什么是进入：单位及其等式

电导率是材料的基本特性，以允许电流流过它们。基于所属材料的导电性，它们被归类为导体，半导体和绝缘体。导体是允许易于电流流动的材料。绝缘体是反对电流流动的材料，因此没有电流通过它们。电流流量导体允许取决于材料的电导率。因此，使用称为“导纳”的数量测量电流可以允许电流流动容易。

什么是入场？

入场是指导数量，告诉我们导电装置如何允许电流流过它。电路的电阻被定义为电路的特性，由其与电流的流动相反。抵抗性只有幅度，没有阶段。在处理AC电路时使用正弦信号。因此，代替电阻，阻抗用于测量交流电路中的电阻。阻抗类似于电阻但与电阻不同，它具有幅度和相位。

阻抗方程的实部提供电路的电阻值。虚部阻抗方程代表电路的电抗部分。入场可以定义为阻抗的互惠。导纳测量电路允许的电流流，这是阻抗功能的反比。

除了材料的电导之外，导纳价还取决于电路的遗传。材料的遗传被定义为它允许其允许流过其流动的变化的易容易性。它由字母 - B表示。遗传是反应的反比。

单位

通过对材料的电导和遗传的组合来源。交流电路的电导表示为“G”，其单位是'MHO'。遗传是进入的虚构部分，由符号'B'表示。遗传单位类似于电导“MHO”的单位。在现代的日子里，使用适当的测量单位'西门子'而不是'MHO'。电容敏感性是负值，而感应遗传是正价值。

在交流电路中，导纳用符号'y'表示。入场单位是“西门子”类似于电导单位。“入场”这个词是英语工程师，物理学家和数学家奥利弗在1887年使用的。

公式

入场是一个复杂的数字。它具有真正的部分和虚构部分。电导'g'形成等式的真实部分，而遗传'b'则形成导纳的虚部。因此，入场的公式是

y = g + jb

在这里，Y是西门子的导纳，G是西门子的电导，B在西门子的遗传。

电导是电阻的倒数，所以，对于AC电路G可以写为G = R /（r²+ X.²）。这里，R表示交流电路的电阻，x表示交流电路的电抗。类似地，对于AC电路频率，可以从电阻和电抗值计算

b = -x /（r²+ X.²），它是消极的电容器遗传和阳性电感器遗传。

从阻抗的进入衍生

使用AC电路的电阻和电抗值计算阻抗'Z'。阻抗是一个复杂的数字。电路的电阻'R'形成阻抗方程的实部。电抗'x'形成阻抗方程的虚部。

阻抗的公式是z = r + jx。

进入AC电路是阻抗的互惠。使用阻抗值可以容易地推导出电路的导纳值。

入场的y'可以测量为y = 1 / z

其中'z'是阻抗，z = r + jx。因此，可以写入y = 1 / r + jx。

因此，当衍生自阻抗时的导纳的公式是，y =（r-jx /（r²+ X.²）））。

∠y= arctan（-x / r）= arctan（b / g）

入场三角形

为了更好地理解导纳的相位和幅度并测量各种其他相关数量，使用终止三角形。它在X轴处的电导'G'形成，在Y轴处的沟通'B'，并在X轴处形成具有电导率的角度φ。

下图显示了导纳三角形。

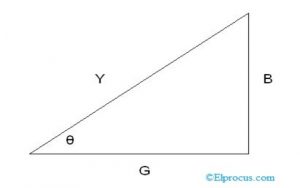
从三角形，

tanφ= b / g

Cosφ= G / Y，这是功率因数的量度

i = v×y，其中我表示所得到的电流。

在串联电路中纳入

下图显示了具有串联电阻和电感电抗的AC电路。

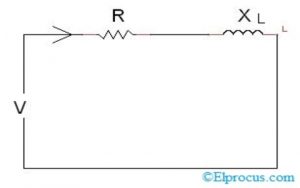
这里r =电阻，x_L.=电感抵抗力。

y = 1 / z

= 1 / R + JX_L.

=（r-jx_L./（r²+ X.²_L.）

= r /（r²+ X.²_L.）-JX._L./（r.²+ X.²_L.）

我们知道AC电路中的电导率可以写为R /（R.²+ X.²_L.）掌管'b'可以写作x_L./（r.²+ X.²_L.）。

因此y = r /（r²+ X.²_L.）-JX._L./（r.²+ X.²_L.）可以写作y = g-jb_L.。在这里b_L.是电感电路的遗传。

类似地，可以推导出含有串联导纳的电阻和导电电抗的电路。在这里，X._C表示电路的导电电抗。

因此，'y'可以写成y = r /（r²+ X.²_C）+ JX._C/（r.²+ X.²_C）

因此，y = g + jb_C，其中B._C是导体电路的易感性。导电频率是负值，而感应频率是正值。

平行电路

下图显示了具有两个分支A和B的平行电路。

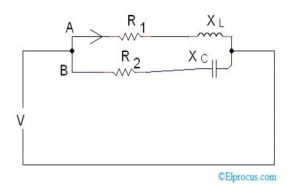
分支机构'a'由x的电感器x组成_L.与具有电阻的电阻串联连接₁'。分支机构'a'与分支'b'并行连接。分支'B'由具有电容电抗x的电容器组成_C与具有电阻的电阻串联串联₂'。

电压V应用于电路。对于分支机构'A'，指导'G'计算为，

G₁= R.₁/ R.₁²+ X.²_L.

= R.₁/ Z.₁²，这里z.₁是阻碍的

分支机构的遗传学计算为B._L.= X._L./ R.₁²+ X.²_L.

。即B._L.= X._L./ Z.₁²

因此，'y₁'= G.₁-J B._L.

= R.₁/ Z.₁²- J X._L./ Z.₁²

同样对于分支'B'，电导'G₂'= R.₂/ Z.₂²，其中r₂是分支'b'的阻力

Z.₂是分支'B'的阻抗。导电疯狂的b_C'对于分支'b'计算为b_C= X._C/ Z.₂²，其中'x_C'是分支导体的导电电抗。因此，入境₂'Branch'b'是作为'y₂'= G.₂+ JB._C

因此，可以计算平行电路的总导纳作为每个分支的导纳的量量。因此，总导入y = y₁+ Y.₂

=√（r₁/ Z.₁²+ R.₂/ Z.₂²）²+（X._L./ Z.₁²-X_C/ Z.₂²）²

在设计期间变形金刚和传输线路，分流元件发挥着重要作用。分流部件为传输线和变压器中的电流流动提供最小电阻的路径。这些分流组件在其导纳值方面指定。这些分流器部件存在于变压器的每一侧。在简化的变压器分析期间，可以忽略分流部件的导纳。是什么形成导纳方程的虚构部分？