毕奥萨伐尔定律及其应用实例

比奥萨伐尔定律指出，它是一个数学表达式，说明磁场产生的稳定电流在特殊的电磁学中。它告诉磁场大小，长度，方向，以及电流的接近程度。该定律是静磁学的基础，在静电学中起着与库仑定律相关的重要作用。每当磁静力学不适用时，这个定律就必须用杰菲门科方程来改变。该定律适用于静磁估计，且具有高斯(磁性)和安培(环路)定律的可靠性。来自法国的两位物理学家，Jean Baptiste Biot和Felix Savart，实现了磁通密度接近于a的精确表达式载流导体1820年。通过筛选磁罗盘指针的偏转，两位科学家完成了对空间中每一个电流分量的估算(S)。

什么是毕奥萨伐尔定律?

携带长度为dl的电流I的导体是基本的磁场源。另一个相关导体上的功率可以很容易地用初级导体产生的磁场(dB)来表示。磁场dB依赖于“I”电流、尺寸以及长度方向dl和距离r，这主要是由Biot & Savart估计的。

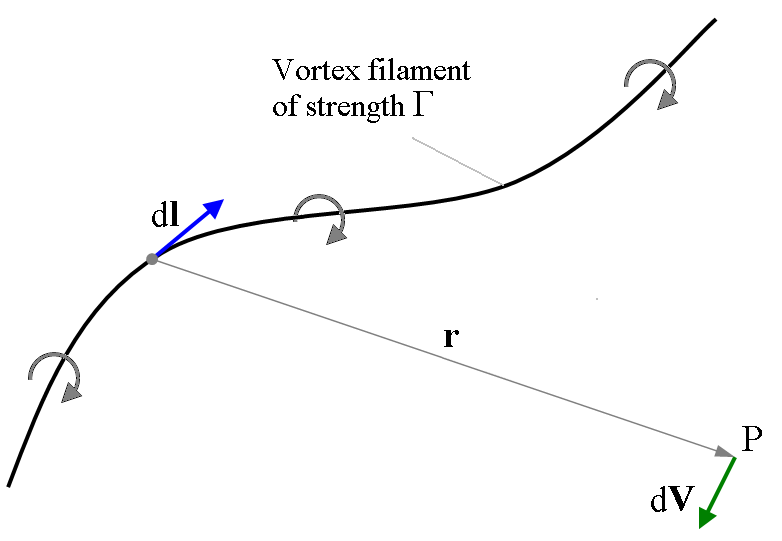
一旦从端到端观察以及计算派生一个表达式,包括磁通密度(dB)成正比的元素长度(dl)的流动电流(I),θ角的正弦电流的流动方向和磁场的向量结合给定的位置,与当前组件与指定点到当前元素的距离(r)的平方成反比。这是Biot Savart法律声明。

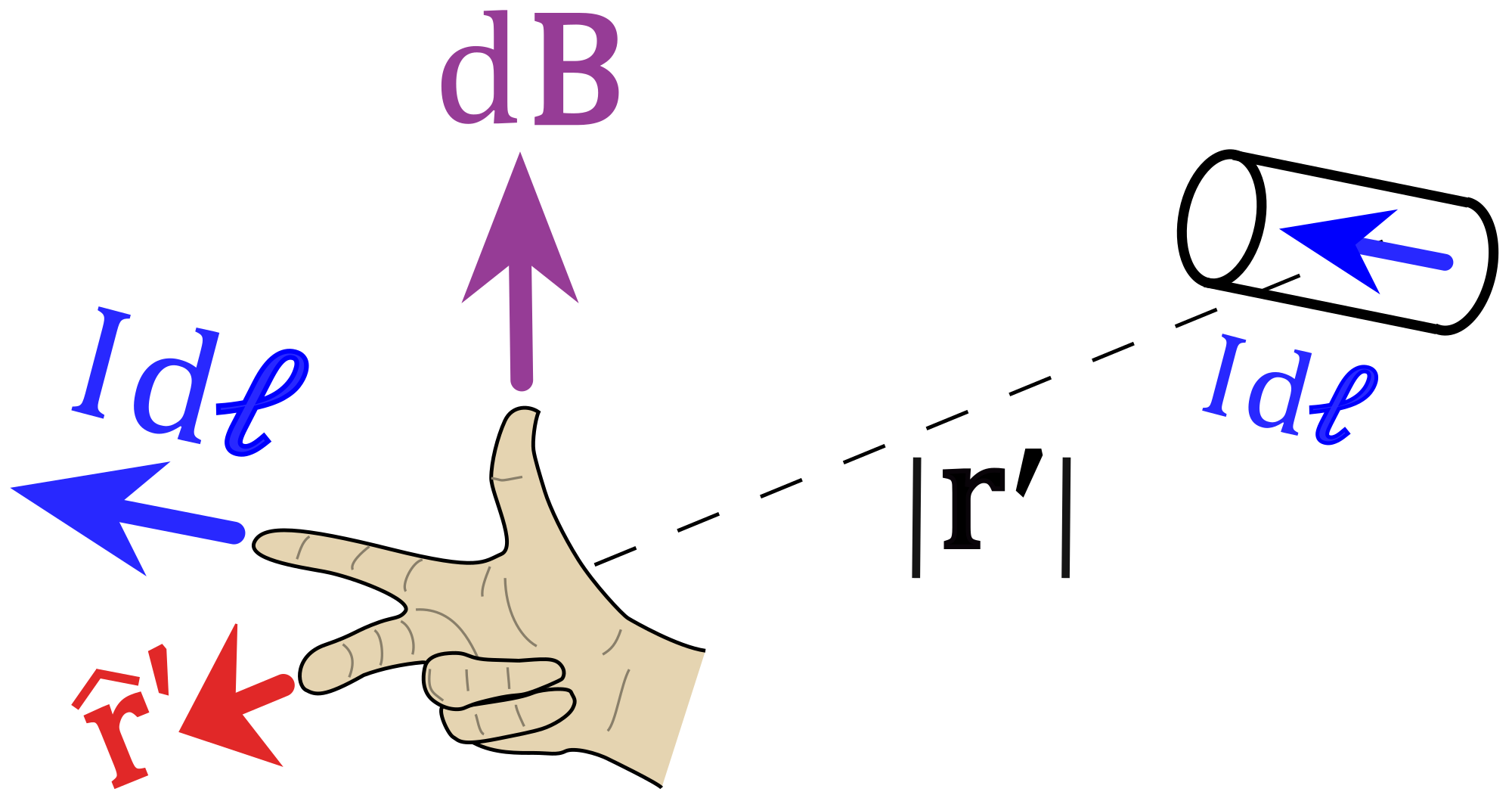
因此，dB与sinθ/ r成正比²也可以写成dB = k Idl sinθ / r²

dH = μ0 μr/4п x Idl Sin θ/ r²

dH = kxidl Sin θ/ r²(式中k= μ0 μr/4п)

dH正比于Idl Sin θ/ r²

这里，k是一个常数，因此毕奥-萨伐尔定律的最终表达式为

dB = μ0 μr/4п x Idl Sinθ/r²

比奥萨伐尔定律数学表示

让我们检查一个长电流携带(I)电线和一个端P在空间。载流导线在图中以特定的颜色显示。让我们也考虑一小段导线(dl)，从P端到r的距离如图所示。在这里，距离矢量(r)根据电流在导线一小段中的路径形成一个θ角。

如果你想想象这种情况，我们可以简单地知道P点端点的磁场密度，因为导线的微小长度dl，与导线这部分的电流成正比。

当整个导线的电流与整个导线本身所携带的电流相似时，可以记为

dB∝我

我们也可以很正常地想象，由极短的导线引起的P端磁场的密度，与从P端到dl中间的直接距离的平方成反比。这个可以写成，

dB∝1 / r²

最后，P点末端的磁场密度与导线的实际长度成正比。距离矢量r之间的夹角θ以及流经dl导线这一小段的电流方向，dl导线垂直于末端P的分量是dlSinθ。

因此,dB∝dl罪θ

现在，把这三个宣言结合起来，我们可以这样写:

dB∝I.dl .Sinθ/ r²

上面的比奥萨伐尔定律方程基本类型是什么毕奥萨伐尔定律。目前，将常数(K)值代入上式，可得:

dB = k Idl sinθ/ r²

dB = μ0 μr/4п x Idl Sinθ/r²

其中，常数k取μ0为真空的完全渗透率，μ0的值为4π10⁷以SI为单位的Wb/A-m和μr为介质的相对渗透率。

目前，由载流导线全长引起的P端B(通量密度)可表示为:

∫dB =∫μr/4п x Idl Sinθ/r²= I μ0 μr/4п∫Sinθ/r²戴斯。莱纳姆:

如果距离D垂直于终点P，那么它可以写成

r罪θ = D => r = D/罪θ

因此，' P '端B(通量密度)可以重写为:

B = I μ0 μr/4п∫Sinθ/r²dl = I μ0 μr/4п∫Sin^3.θ/D²戴斯。莱纳姆:

再说一次,床θ = l/D，则l = Dcotθ

根据上图

因此，dl = -D csc²θdθ

最后，通量密度方程为

B = I μ0 μr/4п∫Sin^3.θ/D²(- d csc²θdθ)

B = -I μ0 μr/4пD∫Sin^3.θcsc²θ dθ => -I μ0 μr/4пD∫Sinθdθ

该θ角取决于载流导线的长度以及p点。对于特定的不完全长度的载流导线，上图中的θ角由角度θ变化而来₁角θ₂。因此，由于导线长度的关系，P端磁通密度为:

B =4 - 0μμr /пD

-I μ0 μr/4пD [-Cos= I μ0 μr/4пD [Cos .]

假设载电流的导线很长那么角度就会改变θ1到θ2(0 -π)。将这些值代入上式毕奥萨伐尔定律，然后我们可以得到下面的final毕奥萨伐尔定律推导。

B =I μ0 μr/4пD [Cos= I μ0 μr/4пD [1= I μ0 μr/2пD

Biot Savart法律例子

圆形线圈有10圈，半径为1米。如果通过它的电流是5A，那么从2m的距离确定线圈中的磁场。

• 转数n= 10
• 目前的5
• 长度= 2米
• 半径= 1米
• 的毕奥萨伐尔法律声明是由,
• B = (μo / 4π) × (2πnI / r)
• 然后将上述值代入上式
• B =(μo / 4π)×(2×π10××5/1)= 314.16×10 - 7 T结果

毕奥萨伐尔法律应用

的应用毕奥萨伐尔定律包括以下

• 这一定律甚至可以用于计算分子或原子水平上的磁反应。
• 它可用于气动理论中确定涡线激励的速度。

因此，这就是毕奥萨伐尔定律。最后由上述信息，我们可以得出结论，由电流单元引起的磁场可以用这一定律计算出来。并且，由于某些结构，如圆形线圈，圆盘，线段，磁场是用这一定律确定的。毕奥萨伐尔定律的作用是什么吗?