什么是代码转换器：二进制文件到灰色代码和灰色代码到二进制转换

在计算机中，我们需要将二进制文件转换为灰色和灰色到二进制。可以通过使用两个规则来完成这一点的转换，即二进制到灰色转换和灰色到二进制转换。在第一个转换中，格雷码的MSB不断等同于二进制代码的MSB。额外的格雷代码输出位可以使用前或逻辑门概念来到本指数索引以及早期索引的二进制代码。这里的MSB只不过是最重要的位。在第一转换中，二进制代码的MSB不断等同于特定二进制代码的MSB。二进制代码的输出的其他位可以使用前或逻辑门通过验证当前索引的灰度代码来概念。如果当前的灰码位为零，则在缩短之前复制二进制代码，以及早期二进制代码位的复制反转。本文讨论了代码转换器的概述，该代码转换器包括二进制文件到灰色代码转换器以及灰色到二进制代码转换器。

什么是二进制代码？

在数字计算机中，基于二进制数字系统的代码被称为二进制代码。有两种可能的状态，比如通过0和1表示的ON和OFF。数字系统使用10位数字，每个数字的位置表示10的幂。在二进制系统中，一位数字的每个位置都代表2的乘方。

二进制代码信号包括一系列表示要执行的字符、数字和操作的电脉冲。时钟装置用于传输普通脉冲，以及晶体管等元件，打开/关闭以流动，否则会阻塞信号。在二进制代码中，从0到9的每个十进制数都可以通过一组4位二进制位/数字来表示。基本的加法、减法、乘法和除法运算都可以简化为二进制数上的基本布尔代数函数的组合。

什么是灰色密码?

灰色代码或RBC（反射二进制代码）或循环代码是一系列二进制数字系统。调用此反映二进制代码的主要原因是初始N / 2值与与最后一个数字值相比相反的顺序。在这种代码中，两个连续的值通过单一的二进制数字改变。这些代码主要用于硬件生成的共同系列二进制数。

二进制数一旦从单个数过渡到连续数，就会产生错误。这种类型的代码基本上解决了这个问题，只要在数字之间改变一个位。

这种代码是非常轻的权重&它不依赖于整个位置声明的数字值。这种代码也被称为循环变量代码，因为单个值对其连续值的变化只包含一个比特的变化。

这是单位距离代码最受欢迎的;但是，它不适用于算术函数。灰色码的应用包括模拟与数字转换器和用于纠错的数字通信。bob的是什么网站首先，灰色代码不容易理解，然而，变成非常容易识别。

二进制到灰色代码转换器

二进制代码是使用两个值的非常简单的数据表示，例如0和1，它主要用于计算机的世界。二进制代码可以是高（1）或低（0）值，也可以是甚至是值的均匀修改。灰色代码或反射二进制代码估计与开启和关闭指示器排列的二进制代码性质，通常用Zeros表示。这些代码用于查看清晰度以及二进制中的错误修改bob的是什么网站通信．

将二进制码转换为灰色码可以通过使用逻辑电路．格雷代码是非加权代码，因为没有特别重量为该位的位置分配。可以通过在2的行之后再现n-1位代码来实现n位代码^{n - 1}，以及将最高有效位0放在轴上，最高有效位1放在轴下。逐步生成灰色代码如下所示。

该方法使用EX-OR GATE在二进制比特中执行。以下最佳示例对于知道二进制到灰色的转换非常有用。在这种转换方法中，取下当前二进制数的MSB位，因为灰色代码号的主位或MSB位类似于二进制数。

连续的灰色编码比特生成相应的灰色给定二进制数字编码的位数,添加主位或MSB二进制数的位数向第二位&记下旁边的产品主要格雷码,然后添加下一个二进制位,第三位记下旁边的产品2ⁿ一个灰色的代码。类似地，遵循这个过程直到最后的二进制位，并记下所依赖的结果前或逻辑操作生成相应的灰色编码二进制数字。

灰色码转换器的二进制文件示例

假设二进制码位为BO，B1，B2，B3，而可以基于以下概念实现特定的格雷码。

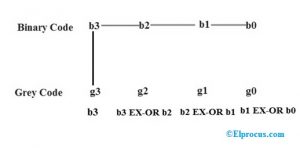
从上述操作中，最后我们可以获得G3 = B3，G2 = B3 XOR B2，G1 = B2 XOR B1，G0 = B1 XOR B0等灰度值。

例如，取二进制值b3, b2, b1, b0 = 1101，并根据上述概念找到灰色代码g3, g2, g1, g0

g3 = b3 = 1

G2 = B3 XOR B2 = 1 XOR 1 = 0

g1= b2 XOR b1= 1 XOR 0 = 1

g0= b1 XOR b0= 0

二进制1101的值的最终的灰度代码是1011

二进制到灰色代码转换表

十进制数	二进制代码	灰色代码
0	0000	0000
1	0001	0001
2	0010	0011
3.	0011	0010
4	0100.	0110
5	0101	0111
6	0110	0101
7	0111	0100.
8	1000	1100
9	1001	1101
10	1010	1111
11	1011	1110
12	1100	1010
13	1101	1011
14	1110	1001
15	1111	1000

VHDL代码为二进制到格雷码转换在下面给出。

图书馆ieee;
使用ieee.std_logic_1164.ALL;
实体bin2gray是
端口（bin：在std_logic_vector（3 downto 0）; - 中华输入
g：out std_logic_vector（3 downto 0）-Gray代码输出
）;
bin2gray结束;
Bin2Gray的体系结构门_LEVEL是
开始
xor门。
g（3）<=箱（3）;
G(2) <= bin(3) xor bin(2);
g（1）<=箱（2）XOR箱（1）;
g（0）<=箱（1）XOR箱（0）;
结尾;

优点

的二进制码的优点包括以下这些。

• 使用二进制代码的主要好处是它只是通过电子设备表示
• 二进制数据存储也很简单。
• 非常容易表示和控制电子和机械。
• 可以增加符号表示之间的差异，从而减少错误的可能性。

的二进制代码的缺点包括以下这些。

• 可以增加所需的符号数以表示给定数量的整体位置值系统。
• 由于它们的长度和默认使用10进制数字，人类无法非常有效地阅读它们
• 它使用许多数字来表示任何逻辑号

应用程序

二进制代码的应用包括以下内容。

• 二进制代码用于电信以及计算与位字符串相同的数据编码的数据的bob的是什么网站不同技术。这些方法使用的宽度是固定的其他变量宽度字符串。
• 这在计算机语言和程序设计中使用，因为计算机语言主要依赖于两位数系统。

灰色到二进制代码转换器

这种灰色到二进制转换方法还使用灰色等位和二进制位之间的前逻辑门的工作概念。以下示例逐步步骤过程可以有助于将灰色代码的转换概念知识到二进制代码。

要将灰色更改为二进制代码，请取下灰色代码号的MSB数字，因为初级数字或格雷代码的MSB类似于二进制数字。

为了得到下一个直接的二进制位，它使用二进制的主位或MSB位到灰码的下一个位之间的异或运算。

类似地，为了获得第三直二进制比特，它使用二进制的第二位或MSB位中的XOR操作到灰色码的第三MSD位等。

二进制代码转换器的灰色示例

我们假设灰色代码数字G3，G2，G1，G0，而特定二进制代码位是BO，则可以基于以下概念实现B1，B2，B3。

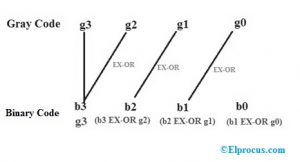
由上面的操作，最后我们可以得到二进制值，如b3 = g3, b2 = b3 XOR g2, b1= b2 XOR g1, b0 = b1 XOR g0。

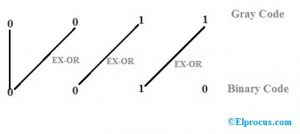
例如，拍摄灰度值G3，G2，G1，G0 = 0011并根据上述概念找到二进制代码B3，B2，B1，B0

b3 = g3 = 0

B2 = B3 XOR G2 = 0 XOR 0 = 0

B1 = B2 XOR G1 = 0 XOR 1 = 1

b0 = b1 xor g0 = 1 xor 1 = 0

灰色0011值的最终二进制代码是0010

灰色到二进制代码转换器表

十进制数	灰色代码	二进制代码
0	0000	0000
1	0001	0001
2	0010	0010
3.	0011	0011
4	0110	0100.
5	0111	0101
6	0101	0110
7	0100.	0111
8	1100	1000
9	1101	1001
10	1111	1010
11	1110	1011
12	1010	1100
13	1011	1101
14	1001	1110
15	1000	1111

优点

的灰码的优点包括以下这些。

• 可以减少逻辑电路
• 用于交叉时钟域
• 用于将模拟信号转换为数字信号时减小误差
• 一旦在遗传算法中使用它，就可以减少汉明墙的发生。

缺点

格雷码的缺点包括以下内容。

• 不适用于算术函数
• 适用于一些精确的应用程序

应用程序

灰色代码的应用包括以下几个方面。

• 它被用于模拟到数字转换器
• 在数字通信中，用于校正bob的是什么网站错误
• 它在将信号从模拟变为数字时减少错误。
• 数学谜题
• 最小化布尔电路
• 它用于两个时钟域之间的通信bob的是什么网站
• 遗传算法
• 位置编码器

vhdl代码为二进制转换的灰色代码在下面给出。

图书馆ieee;
使用ieee.std_logic_1164.ALL;
实体gray2bin是
端口（g：在std_logic_vector（3 downto 0）; -Gray代码输入
bin：out std_logic_vector（3 downto 0）-binary输出
）;
结束Gray2bin;
灰色2bin的体系结构gate_level是
开始
xor门。
bin（3）<= g（3）;
箱（2）<= g（3）xor g（2）;
bin(1) <= G(3) xor G(2) xor G(1);
箱（0）<= G（3）XOR G（2）XOR G（1）XOR G（0）;
结尾;

3位二进制到灰色代码转换器

假设B0，B1，B2等3位二进制数中的二进制数字，无论'B2'位是MSB（大大有效位），'B0'位是二进制的LSB（最低有效位）。灰色代码的数字是G0，G1，G2，无论'G2'数字是MSB（最高有效位），而数字'G0'是格雷代码的LSB（最低有效位）。

二进制代码 - B2，B1，B0	格雷代码- g2,g1,g0
000	000
001	001
010	011
011	010
One hundred.	110
101	111
110	101
111	One hundred.

由此，用k-map求解二进制到灰色码转换器的布尔表达式，得到g2 = b2, g1 = b1⊕b2 & g0 = b0⊕b1。同样，我们可以将n位二进制数(bnb (n-1)…b2 b1 b0)转换为Gray码(gng (n-1)…g2 g1 g0)。

对于LSB（最重要的位）

g0 =b0⊕b1.

g1 = b1⊕b2

g2 = b1⊕b2

G (n-1) = b (n-1)⊕bn, gn = bn。

例如，将111010二进制数转换为格雷码。

基于上述算法，

G0 = B0⊕B1=> 0°1 = 1

G1 = B1⊕B2=1¼0= 1

G2 = b2⊕b3 = 0⊕1 = 1

⊕1 = 0

⊕1 = 0

g5 = b5 = 1 = 1

因此，二进制码到灰色码的转换为- 100111。

基于ic7486的二进制到灰度码转换器

二进制到灰色和灰色到二进制的转换可以用IC7486完成。所需的组件包括面包板、连接线、led、电阻、异或(IC7486)、按钮开关和电源电池。

IC7486的包主要包括四个XOR逻辑门，其中引脚7和14将为所有逻辑门提供电源。单个XOR门的O / PS连接到相同或其他芯片内的其他逻辑门的输入，直到它们共享类似的接地终端。

因此，这是关于二进制到灰色代码转换器和灰色到二进制代码转换器的。从上面的信息结束，我们可以得出结论这些转换器在执行不同的操作中扮演重要的角色数字电子产品bob足球体育app以及各种数字系统之间的bob的是什么网站通信。我们上面讨论的代码转换器示例可能有助于了解如何执行这些计算的概念。这是一个问题，灰度代码的应用是什么？