什么是完全减法:使用逻辑门的结构

一般来说，全减法是最常用的和之一基本组合逻辑电路。它是一种基本的电子设备，用于执行两个二进制数的减法。在早期的文章中，我们已经给了基本理论半加法器&全加法器它使用二进制数字进行计算。同样，全减法使用像0,1这样的二进制数字进行减法。这种电路可以用逻辑门如或、异或、与非门组成。这个减法的输入是A, B, Bin输出是D, Bout。

本文给出了一个完整的减法器理论思想，包括什么是减法器、用逻辑门设计、真值表等前提。这篇文章是有用的工程学生谁可以通过这些主题在HDL实践实验室。

什么是减法?

二进制数字的减法可以借助减法电路来完成。这是一种组合逻辑电路，用于执行两个二进制数字的减法，如0和1。从0到0或从0到1的二进制数的减法不会改变结果，从1到1的减法会得到0，但是从1到0的减法需要借位。

例如，2位减法器电路包括两个输入，如A和B，而输出是差和借用。该电路可以用加法器和位于每个数据输入以及FA早期借用(Bin)输入之间的逆变器来构建。

减法器分为两种类型，如半部减法器和全减法器。在这里，我们正在讨论完整的减法者。

什么是全减法?

它是一种电子设备或逻辑电路它执行两位二进制数字的减法。它是数字电子设备中使用的组合逻辑电路。bob足球体育app许多组合电路可用集成电路技术即加法器、编码器、解码器和多路复用器。在这篇文章中，我们将讨论用半减法和真值表等项来构造它。

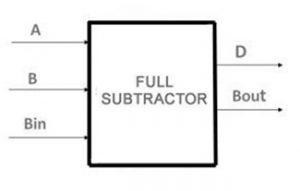
采用两个半减法进行设计，包括减法、借位和减法三个输入，输入之间的借位由两个二进制数字相减得到，再由下一个高阶位对减去，输出为差和借位。

的完整的减法器块图如下所示。半减法器的最重要缺点是，我们不能在这个减法者中借用借款。虽然在其设计中，实际上我们可以在电路中借用借款，并可减去剩余的两个I / PS。这里是Minuend，B是subtrahend＆bin借入。输出是差异（差异）和bout（借用）。完整的减法器电路可以通过使用具有额外或门的两个半减法器获得。

具有逻辑门的全减法器电路图

的使用基本门的全减法器电路图S在以下框图中示出。该电路可以用两个半减法器电路完成。

在最初的半减器电路中，二进制输入是A和b。正如我们在前面的半减器文章中所讨论的，它将产生两个输出，即difference (Diff)和Borrow。

左减法器的差异O / P给出左半减法器电路。差异输出进一步提供给右半减法器电路的输入。我们在下一个其他I / P中提供了借款半减法器电路。再一次，它将给出差异，并借出钻头。该减法器的最终输出是差异输出。

另一方面，两种减法器电路中的借用连接到或逻辑门。晚些时候，除了给出两个输出位的给出或逻辑，我们会从减法器中获取最终借款。最后借用签署MSB（最重要的位）。

如果我们观察它的内部电路，我们可以看到两个带有与非门的半减器和带有一个额外的或门的异或门。

完整的减法器真相表

这减法器电路执行两个位之间的减法，它有3个输入(a, B，和Bin)和两个输出(D和Bout)。这里输入表示减数、减数和前借位，而两个输出表示借位o/p和差值。下图显示了全减子的真值表。

输入			输出
被减数(A)	减数(B)	借(本)	差异(D)	借用（Bout）
0	0	0	0	0
0	0	1	1	1
0	1	0	1	1
0	1	1	0	1
1	0	0	1	0
1	0	1	0	0
1	1	0	0	0
1	1	1	1	1

K-Map

简化的满减法器K-map对于上述差异和借用如下所示。

下面提到了差异的等式以及箱。

差异的表达式是，

d = a'b'bin + ab'bin'+ a'bbin'+ abbin

Borrow的表达式是，

Bout = A 'Bin + A 'B + bin

全减法器电路的级联

前面，我们已经讨论了这类结构的概述，带逻辑门的电路图。但是如果我们想减去两个1位数字，这个减法器电路对于级联单位数字和减去两个以上的二进制数字非常有用。在这种情况下，采用全加法器级联电路，并借助于非逻辑门。电路由全加法器到全减法器的转换可以用2的补码技术实现。

一般情况下，使用非门反全加法器的减数输入，否则为逆变器。通过加上这个被减数(非反向输入)和减数(反向输入)，FA电路的LSB(进位输入)是1，这意味着逻辑高，否则我们使用2的补码技术减去两个二进制数字。FA的输出是Diff位&如果我们倒转执行，然后我们可以得到MSB否则借用位。实际上，我们可以设计出可以观察到输出的电路。

Verilog代码

对于编码部分，首先，我们需要检查逻辑电路图的建模的结构方式。这可以使用AND门，半音，半音电路和逻辑门的组合构建逻辑图，以及逻辑门的组合，或者，而不是XOR门。与结构建模一样，我们向每个基本元素排列解释各种模块。在以下代码中，可以为每个大门定义不同的模块。

该模块适用于或门。

输入:a0,

输出:c0

最后，我们将把这些门精确模块合并成一个单独的模块。为此，这里我们利用了模块的实例化。现在，只要我们想为不同的输入集复制一个精确的模块或函数，就可以使用这个实例化。首先，我们设计了一个半减器，然后利用该模块实现了一个全减器。为了实现这一点，我们使用OR门来组合o/ps变量Bout。的Verilog代码的完整减法器如下所示

模块or_gate(a0, b0, c0);

输入A0，B0;

输出c0;

赋值c0 = a0 | b0;

endmodule

模块xor_gate(a1, b1, c1);

输入a1, b1;

输出C1;

赋值c1 = a1 ^ b1;

endmodule

模块and_gate(a2, b2, c2);

输入A2，B2;

输出C2;

分配C2 = A2和B2;

endmodule

模块not_gate (a3, b3);

输入a3;

输出B3;

分配b3 =〜a3;

endmodule

模块half_subtractor(a4, b4, c4, d4);

输入A4，B4;

输出c4, d4;

x线;

Xor_gate u1(a4, b4, c4);

And_gate u2(x, b4, d4);

not_gate u3 (a4, x);

endmodule

模块full_subtractor(A, B, Bin, D, Bout);

输入A, B, Bin;

输出D，Bout;

Wire P，Q，R;

半减子u4(A, B, p, q);

半减子u5(p, Bin, D, r);

or_gate u6(q, r, Bout);

endmodule

使用4X1多路复用器的全减法器

减法的执行可以通过二的补法来完成。因此，我们需要利用1-异或门，它用于将1位转换为进位。不同的输出类似于完整的加法器电路输出总和然而巴罗o / p不是类似于完整的加法器的进位输出然而倒也称赞,A - B = A + (- B) = A + B的二进制补码。

使用4x1多路复用器的设计如以下逻辑图所示。这种设计可以使用以下步骤完成。

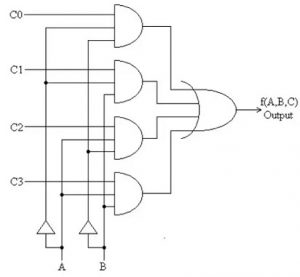
• 在步骤1中，有两个输出如Sub和Bro。所以我们必须选择2个多路复用器。
• 在step2中，真值表可以与k -map一起实现
• 在步骤3中，可以选择这两个变量作为选择线。例如，B和C在这个例子中。

真值表

的全减子的真值表电路使用4x1多路复用器包括以下内容

一个	B	C	子	借
0	0	0	0	0
0	0	1	1	1
0	1	0	1	1
0	1	1	0	1
1	0	0	1	0
1	0	1	0	0
1	1	0	0	0
1	1	1	1	1

使用解码器的全减法器

使用3-8解码器的全减色器的设计可以使用有源低输出来完成。让我们假设解码器使用下面的逻辑图来运行。解码器包括3-8解码器中的3个输入。在真值表的基础上，我们可以写出差值和借值输出的最小项。

根据上面的真值表，

对于真值表中的不同函数，minterms可以写成1,2,4,7，类似地，对于borrow, minterms可以写成1,2,3,7。3-8解码器包括3个输入以及8个输出，就像0到7个数字。

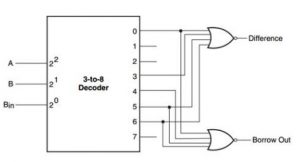
如果减法的输入是000，那么输出' 0 '将是有效的，如果输入是001，那么输出' 1 '将是有效的。

现在减法器的输出可以从1、2、4和7连接到与非门，那么输出就是差值。这些输出可以连接到其他非和逻辑门，在那里输出改变为借用。

例如，如果输入是001，那么输出将是1，这意味着它是活动的。输出是有源的低输出可以通过与非门的差函数得到，比如高借函数也变高了。因此我们得到了首选输出。最后，解码器就像一个完整的减法器。

的优点和缺点

的减法器的优点包括以下。

• 减法器设计简单，实现简单
• DSP(数字信号处理)中的功率扣除
• 计算任务可以高速执行。

的减法的缺点包括以下。

• 在半个减法器中，没有较早阶段接受借用的借阅。
• 减法器的速度可以部分通过电路中的延迟。

应用程序

的一些全减值器的应用包括以下

• 这些通常用于计算机中的ALU（算术逻辑单元），以减去作为图形应用的CPU和GPU以降低电路难度。
• 减法器主要用于执行算术功能，如减法，电子计算器以及数字设备。
• 这些也适用于不同的微控制器用于算术减法、计时器和程序计数器(PC)
• 减法器用于处理器以计算表，地址等。
• 它也适用于DSP和基于网络的系统。
• 这些主要用于计算机中用于减法的ALU，如用于图形应用的CPU和GPU，以降低电路的复杂性。
• 这些主要用于执行算术功能，例如数字设备，计算器等减法。
• 这些减法器也适用于各种微控制器的计时器，PC(程序计数器)和算术减法
• 它们用于处理器计算地址、表等。
• 使用与非门和与非门这样的逻辑门实现这一点可以用任何全减法器逻辑电路来实现，因为NOR和与非门都被称为通用门。

从上面的信息，通过计算加法器，全减器使用两个半减器电路和它的表格形式，可以注意到全减器中的Dout精确地类似于全加法器中的Sout。唯一的变化是A(输入变量)在全减法中得到补。因此，可以将全加法器电路转换为全减法器，只需在i/p a被给定之前对其进行补的逻辑门生成最后一个借位输出(Bout)。

通过使用任何一个全减器逻辑电路，都可以实现使用与非门的全减器和使用nor门的全减器，因为与非门和nor门都被视为通用门。有个问题，半减法和全减法的区别是什么?