什么是谐波振荡器：框图及其类型

简谐运动是由法国数学家拜伦·让·巴蒂斯特·约瑟夫·傅里叶在1822年发明的。Edwin Armstrong(1890年12月18日至1954年2月1日)在1992年的实验中观察到了振荡，Alexander Meissner(1883年9月14日至1958年1月3日)发明了振荡器1993年3月。谐波一词是拉丁语。本文讨论了谐波振荡器的概述，包括其定义，类型及其应用。

什么是谐波振荡器？

谐振子被定义为动力，其中力与来自平衡点的粒子成比例，并且它在正弦波形中产生输出。导致谐波的力量运动能在数学上表示为

f = -kx.

在那里,

f =恢复力

K =弹簧常数

X =到平衡的距离

谐波运动有一个点，其中系统振荡，以及再次在其开始的相同点处再次引起质量的力，力被称为恢复力，并且该点被称为平衡点或平均位置。该振荡器也被称为a线性谐振子。能量从活跃流出组件到振荡器中的无源元件。

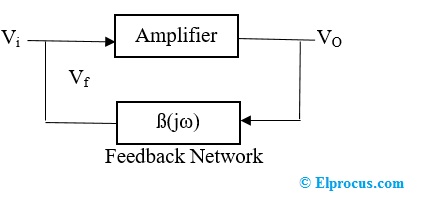
框图

的谐波振荡器的框图由放大器还有一个反馈网络。放大器用于放大信号，被放大的信号通过反馈网络并产生输出。其中Vi为输入电压，Vo为输出电压，Vf为反馈电压。

例子

弹簧上的质量:弹簧提供了加速质量的回复力，回复力表示为

F = ma

m是质量，a是加速度。

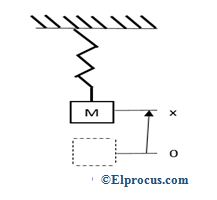
弹簧由质量(m)和力(F)组成。当力在x=0点拉质量，只取决于质量的x -位置，弹簧常数用字母k表示。

谐波振荡器的类型

该振荡器的类型主要包括以下内容。

迫使谐振子

当我们向系统的运动应用外力时，据说运动是强制谐波振荡器。

阻尼谐振子

当我们向系统应用外力时，该振荡器定义为，然后振荡器的运动减小并且其运动被认为是阻尼的谐波运动。它们是有三种类型的阻尼谐波振荡器

在阻尼

当系统朝向平衡点缓慢移动时，据说据说是覆盖的谐波振荡器。

在阻尼

当系统快速向平衡点移动时，我们称它为过阻尼谐振子。

临界阻尼

当系统在不振荡的情况下尽快移动时，据说据说是一个覆盖的谐波振荡器。

量子

它由Max出生，Werner Heisenberg和Wolfgang Pauli在“Gottingen大学”中发明。量子单词是拉丁词，量子的含义是少量能量。

零点能量

零点能量也被称为基态能量。它的定义是基态能量总是大于零，这个概念是由德国的马克斯·普朗克发现的，公式是在1990年发展起来的。

阻尼简单谐波振荡器方程的平均能量

有两种类型的能量，它们是动能和潜在的能量。动能和潜在能量的总和等于总能量。

e = k + u ..................EQ（1）

其中e =总能量

K =动能

U =势能

其中k = k = 1/2 mv²............ eq (2)

u = 1/2 kx²............ eq（3）

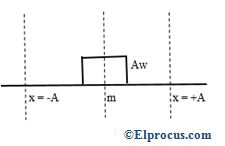
每个振荡周期的动力学和潜在能量的平均值等于

在哪里v²= W.²（一种²-X²)……eq (4)

替代EQ（4）在EQ（2）和EQ（3）中将得到

k = 1/2 m [w²（一种²-X²）

= 1/2 m [Aw cos(wt+ø₀）²......EQ（5）

u = 1/2 kx²

= 1/2 k [仙（wt +Ø₀）²......eq (6)

将eq(1)中的eq(5)和eq(6)代入，得到总能量值

e = 1/2 m [w²（一种²-X²) + 1/2 kx²

= 1/2 m w²-1/2 m w.²一个²+ 1/2 kx.²

= 1/2 m w²一个²+1/2 x²(K-mw²）......eq (7)

在哪里m²= K.，替换在EQ（7）中的这个值

E = 1/2 k a²- 1/2 kx.²+ 1/2 x²= 1/2 k a²

总能量(e) = 1/2 k²

一个时间段的平均能量表示为

K_avg= U._avg= 1/2 (1/2 k a²）

谐振子波函数

Hamiltonian运营商表示为动能和潜在能量的总和，表达为

ђ (Q) = T + V...................eq(1)

其中ђ=哈米尼亚人的运算符

t =动能

v =潜在的能量

要产生波函数，我们必须知道薛定谔方程，方程表示为

-²/2μ* d²ѱ_υ(问)/ dQ²+ 1/2KQ²ѱ_υ（q）= e_υѱ_υ（q）............。EQ（2）

Q =法线坐标的长度

Μ =有效质量

k =力常数

Schrodinger方程边界条件是：

Ѱ(-∞)=ø

ѱ（+∞）= 0

我们也可以写入eq（2）作为

d²ѱ_υ(问)/ dQ²+2μ/ђ²（E._υ- k / 2 * Q²)ѱ_υ(Q) = 0 ............

用于解决方程的参数是

β=ђ/√μk ...........eq (4)

d²/ dQ²= 1 /β²d²/ dx.²............ .. eq（5）

替换EQ（4）和EQ（5）在EQ（3）中，然后该振荡器的微分方程变为

d²ѱ_υ(问)/ dx²+（2μβ.²E_υ/ђ²- X²)ѱ_υ(x) = 0 ...........eq (6)

Power系列的一般表达式是

ΣC¬nx2 .............eq (7)

指数函数表示为

exp (- x²/ 2）............ eq（8）

Eq(7)乘以Eq (8)

ѱυ(x) = ΣC nx2exp (-x2/2) .................eq(9)

通过使用以下等式获得Hermite多项式

ђ_υ(x) = (1)^υ* exp（x²）D / DX^υ* exp（-x²) .................eq (10)

常规常数表示为

N_υ=（1/2^υυ!√Π)^1/2................ eq (11)

的简谐振子解表示为

Ѱ_υ(x) = N_υH_υ(y) e^{-x2 / 2.}.................. eq (12)

其中N_υ是归一化常数

H_υ是Hermite.

e^{-x2 /2}是高斯

等式（12）是谐波振荡器的波形。

该表显示了最低能态的第一项厄米特多项式

υ	0	1	2	3.
Hυ（y）	1	2 y	4 y2-2	8Y.3.-12y.

波浪功能简单的谐波振荡图四个最低能态如下图所示。

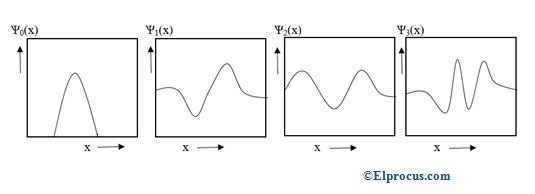
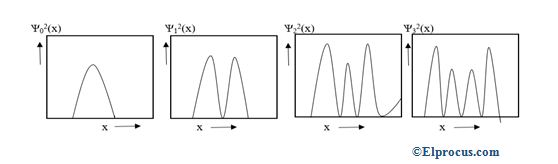
这个振子在四个最低能态下的概率密度如下图所示。

应用程序

的年代谐波振荡器应用主要包括以下内容

• 音频和视频系统
• 无线电和其他通信设备bob的是什么网站
• 逆变器,警报
• 蜂群
• 装饰灯

好处

的谐波振荡器的优点是

• 便宜的
• 高频代
• 高效率
• 便宜的
• 可移植的
• 经济

例子

该振荡器的示例包括以下内容。

• 乐器
• 单摆
• 质量弹簧系统
• 摇摆不定的
• 时钟手的运动
• 汽车，车载车辆，车辆，公共汽车等的运动

它是一种运动，我们可以在我们的日常基地观察。谐波振荡器推导了使用Schrodinger的波浪功能和谐波振荡器的方程。这是一个问题，Bungee跳跃的运动是什么类型的动作？