最大功率传递定理的举例说明

在任何电气和电子电路中，电力供应用于向负载提供电能，无论何时它变为功能性工作。基本上，由于加热效果以及电路内的其他限制，整个电源都不会在负载。因此，绘制和提供权力之间存在一定的差异。负载的大小将影响从电源源传递的电源总和，负载内的任何变化反抗可导致修改内的功率向负荷转移。因此，最大功率传递定理(MPTT)保证了向负载提供最大功率的条件。

在任何电子或电气应用中，通过负载获得的功率总和是一个基本参数。例如，直流电路中的负载可以用a表示电阻器耐抵抗力“RL”欧姆。以同样的方式在交流电路中，我们可以通过具有阻抗'ZL'欧姆的复杂负载来指示它。本文讨论了MPPT（最大功率传输定理）的概述。

什么是最大功率传递定理?

的最大功率传输定理可以定义为载荷电阻时电阻负载连接到DC网络（R._l）相当于内部电阻，然后它收到最高功率被称为源网络的等效电阻。定理定义了在一次源电阻时选择负载电阻（RL）。对将定理应用于反向局势的普遍误解是一般的误解。

这并不意味着如何为一个特定的负载电阻(RL)选择源电阻。实际上，除了负载电阻的值外，最能充分利用功率转移的源电阻始终为零。这个定理可以推广到AC电路包括电抗并且定义最高动力传输在负载阻抗（ZL）等同于Zth（相应电路阻抗的复合缀合物）时发生。

最大功率传输定理解决问题

1).找到使电路(a和b端子左侧)向负载输出最大功率的负载电阻RL。同时，找出负载的最大功率。

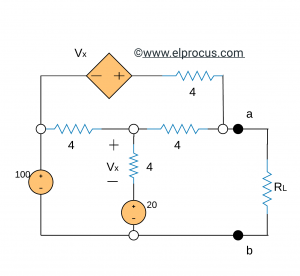
解决方案:

为了应用最大功率传输定理，我们需要找到临时的等效电路。

（a）电路的vth推导：开路电压

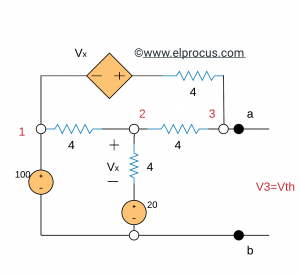
约束:V1=100, V2 - 20=Vx, V3=Vth

节点2:

在节点3:

（1）* 2 +（2）* 3 - > Vth = 120 [V]

（b）RTH推导（通过测试电压方法）：停用和测试后电压的应用程序， 我们有：

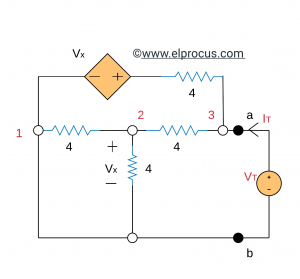
约束：v3 = vt和v2 = vx

节点2:

在节点3（kcl）：

由(1)和(2)起:

(c)最大功率传输:现在电路减少为:

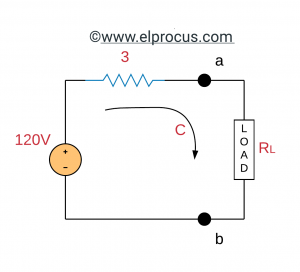
为获得最大的功率传递，则RL=3=Rth。最后，传递给RL的最大功率为:

2）。确定可以传递给的最大功率可变电阻器R。

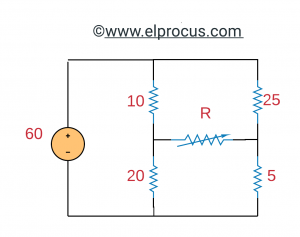
解决方案:

（a）vth：开路电压

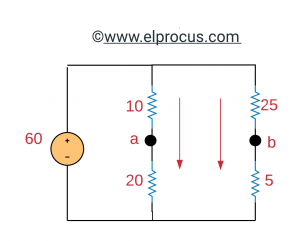
从电路，Vab=Vth=40-10=30 [V]

（b）RTH：让我们应用输入电阻方法：

然后Rab =(10 / / 20) +(25 / / 5) = 6.67 + 4.16 = 10.83 =仅仅。

（c）临时电路：

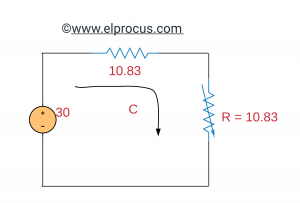
MPTT公式

的最大功率传递定理公式下面的解释。如果我们把η(效率)看作是通过负载溶解的功率的分数R用源延长电源，vth.，那么计算易于计算最大功率传输效率作为

η = (Pmax/P) X 100 = 50%

在那里;最大功率(Pmax)

pmax = V.²_TH.R_{TH / (}R₊R_TH.2._＝V²_{TH /}4R._TH.

提供的电源（P）是

P = 2 v²_{TH /}4R._TH.= V.²_TH./ 2 r_TH.

η达到最高功率转移时，η仅为50％，虽然达到100％作为r_l(负载电阻)达到无穷大，而整个功率级趋于零。

AC电路的最大功率传输定理

在交流电路中，MPTT提供阻抗条件，将最高功率转移到负载。该定理说明，在有源交流电路中，包括一个通过内部阻抗(如ZS)连接到负载(如ZL)的源。因此，当负载阻抗等于ZS或源阻抗的复合共轭时，最大功率转移主要发生在源向负载的转移。

作为非活动布置，最高的功率被传输到负载，而负载的阻抗等效于从负载的终端观察到的给定装置的相应阻抗的复共轭。

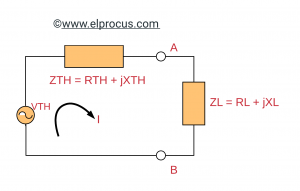
上述电路是临时的等效电路。当上述电路横跨负载端子时，将给出电流的流量

I = VTH / ZTH + zl

其中zl = rl + jxl

zth = rth + jxth

所以，

I = VTH / (RL + jXL + RTH + jXTH)

= VTH / ((RL+ RTH) + j(XL + XTH))

电力循环到负载，

Pl = i2 rl

PL = V2TH×RL /（（RL + RTH）2 +（XL + XTH）2）......（1）

对于最高功率，上述等式衍生物应该是零，而不是简化，我们可以得到以下内容。

xl + xth = 0

xl = - xth

替换上述等式1中的XL值，然后我们可以得到以下内容。

Pl = v2th × rl / ((rl + rth) 2

再次为最高功率传输，上述等式导出必须等同于零，在解决此后，我们可以得到

RL + Rth = 2 RL

RL = Rth.

因此，在交流电路中，如果RL(负载电阻)= RTH & XL = - XTH，则最高功率将从源传输到负载。这意味着负载阻抗(ZL)必须等效于ZTH(相应电路阻抗的复共轭)

zl = zth.

最大传输功率(Pmax) = V2TH/ 4rl或V2TH/ 4rth

直流电路的最大功率传递定理

MPTT用于直流电路，它定义了从有源网络到外部负载电阻的最高功率转移的声明。它定义了在有源、线性、双向直流n/w中，一旦外部负载电阻等于电源的内阻，最高的功率将从电源输出到负载。

可以通过参考电压源或实用电流来实现MPTT的开发。如果电源是独立电压源或实用，则其内部串联电阻应等于负载电阻以传输最高功率。

独立电流源或实用，平行的内阻必须等于负载电阻。DC电路中的内部源串联电阻会改变传输到负载的功率，因此限制从电源传输的最高电流被限制。

MPTT证明

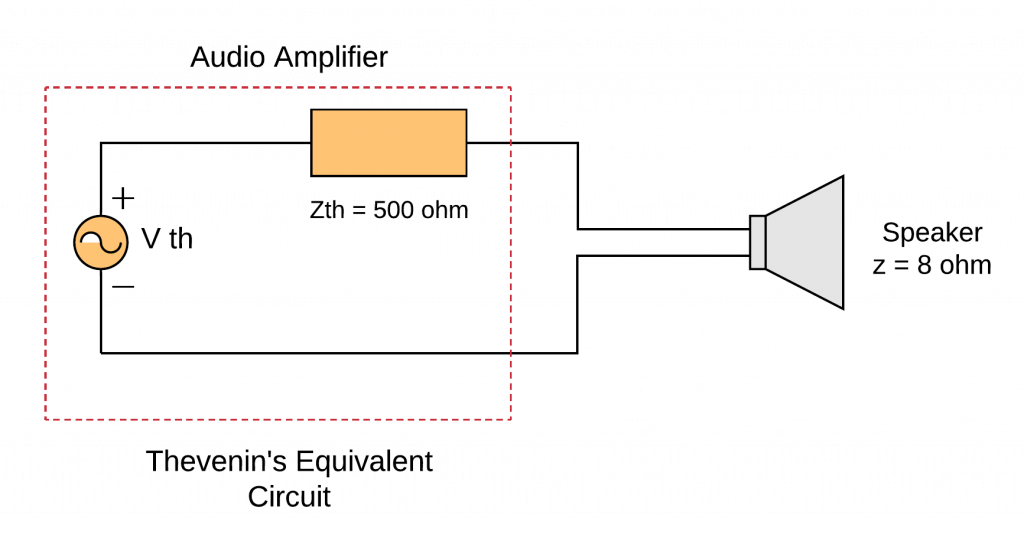
的最大功率传递定理的证明在某些应用中，电路的目的是为负载提供最大功率。一些例子：

• 音响放大器
• 无线电发射器
• bob的是什么网站通信设备

若将整个电路替换为其戴文宁等效电路，除负载外，如下图所示，负载吸收的功率为:

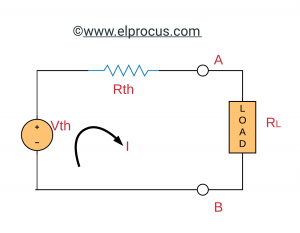
P_l= I.²R_l= (V_TH./ R_TH.+ R_l）²x R._l= V.²_TH.R_l/（r._TH.+ R_l）²

由于VTH和RTH对于给定的电路是固定的，负载功率是负载电阻RL的函数。

通过将PL相对于R1区分并将结果设置为零，我们具有以下最大功率传输定理;当RL等于RTH时，会发生最大功率。

当满足最大功率传输条件时，即，RL = RTH，传输的最大功率是：

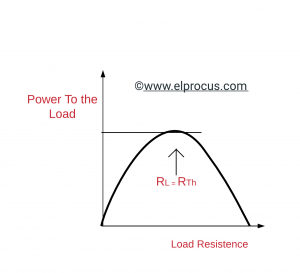
P_l= V.²_TH.R_l/ [r._TH.+ R_l］²= V.²_TH.R_TH./ [r._TH.+ R_l］²= V.²_TH./ 4 R._TH.

用最大功率传递定理求解网络的步骤

以下步骤用于通过最大功率传输定理来解决问题

步骤1:消除电路的负载电阻。

步骤2:通过开放式负载终端查找源网络的源网络的电阻（RTH）。

步骤3:根据最大功率传输定理，Rth是网络的负载电阻，即允许最大功率传输的RL = RTH。

步骤4:最大功率传输由下式计算

（PMAX）= V2TH / 4 RTH

最大功率传输定理解决方案问题

找到以下电路的RL值，即电源最高，使用最大功率传输定理找到最高功率。

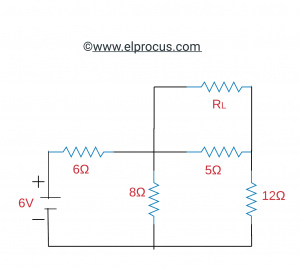
解决方案:

根据该定理，当通过负载的功率最高时，电阻类似于在消除它之后R1的两端之间的等电阻。

因此，对于负载电阻(RL)的发现，我们必须发现等效电阻:

所以，

现在，为了通过rl负载电阻来发现最高功率，我们必须找到VOC电路之间的电压值。

对于上述电路，应用网格分析。我们可以得到:

为Loop-1应用KVL：

6-6i1-8i1 + 8i2 = 0

-14i1 + 8i2 = -6∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙（1）

2回路申请KVL:

8 i2-5i2-12i2 i1 + 8 = 0

8i1-25i2 = 0∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙（2）

通过解上述两个方程，我们得到

I1 = 0.524 a

参考答案

现在，vo。c是

b = 0

vo.c / vab = 5i2 = 5x0.167 = 0.835V

因此，通过负载电阻(RL)的最大功率为;

p max = v_OC²/ 4 r_l=（0.835 x 0.835）/ 4 x 3.77 = 0.046瓦特

发现可以传输到以下电路的RL负载电阻的最高功率。

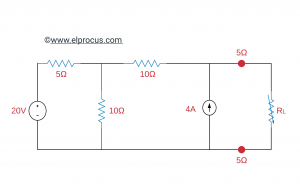
解决方案

将紫色的定理应用于上述电路，

这里，戴文的电压(Vth)=(200/3)，戴文的电阻(Rth)=(40/3)Ω

替换电路的馏分，这是具有临时的等效电路的给定电路的端子A＆B的左侧。二次电路图如下所示。

我们可以通过使用以下公式找到将送到负载电阻的最大功率，RL。

PL，MAX = V2TH / 4 RTH

将VTh = (200/3)V, RTh = (40/3)Ω代入式中。

PL，MAX =（200/3）²/ 4（40/3）= 250/3瓦特

因此，给定电路的负载电阻RL的最大输出功率为250/ 3w。

的优点和缺点

最大功率传输定理的优点和缺点包括以下内容。

• 最大功率传递定理的主要好处是，它可以分析任意点的性能
• 最大功率传输定理的主要缺点是，它不在非线性以及单侧等网络中使用。
• 最大功率传递定理的局限性在于它的效率为50%，不适用于电力系统。所以主要的问题是效率。
• 这个定理可以应用到通信线路而不是电力线上，因为如果应用到电力线bob的是什么网站上，就会出现如下实际问题。
• 在电力线路中，接收端电压恒定是一个很大的条件，因此本定理忽略了此功能。
• 由于效率较低，这不能在电力线内被接受。

最大功率传递定理的应用

定理的最大功率传输可以在许多方面适用，以确定负载电阻的值，该值接收来自电源的最大功率和最高功率传输状态下的最大功率。以下是最大功率传输定理的一些应用：

• 该定理总是在通信系统中寻求。bob的是什么网站例如，在一个社区地址系统中，电路用于最高功率传输，使扬声器（负载电阻）相当于放大器（源电阻）。当负载和源匹配时，它具有相同的电阻。
• 在汽车发动机中，传输到汽车的电动机启动器的电源取决于电动机的有效电阻和电池的内部电阻。当两种电阻等同时，那么最高功率将被传输到电动机以激活发动机。
• 最大功率传递定理可以应用在复杂网络中
• 它用于AC和DC网络。
• 为了在公共广播系统中实现最大功率传输，可以通过使RL(负载电阻)像扬声器一样等效于放大器的源电阻来改变电路。一旦源和负载都包含等效电阻，那么它们就进行匹配。
• 这个定理适用于所有的自主电压源失效的地方&简单地考虑相同的阻抗，然后可以传输最大的功率。
• 在无线电通信中，如bob的是什么网站果电路内的负载阻抗相当于源的阻抗，则功率放大器向天线广播最高信号的位置。
• 在音频系统中，使用它需要向扬声器传送的地方。一旦负载阻抗相当于源阻抗，放大器会更换最高的声音。
• 在电阻性网络中，当负载电阻与通过负载观察到的电阻相等时，电阻性负载将提取出最大功率，因为它向后看向网络。
  实际上，可以向网络输出端访问电阻。实际上，如果我们考虑像电压源的完整网络，那么这种阻力是在临时定理中描述的等效电阻。同样，如果我们考虑像电流源类似的网络，那么这种电阻将被称为Norton等效电阻，这可以在Norton定理中描述。
• 它适用于所有基于效率原理设计的电路，可以降低50%的效率。然而，消费者在电力受到限制的地区使用这种MPTT，如移动接收器和音频扬声器。
• 为了向网络中使用的负载提供最高的电力，这种低效率是可以忍受的。在电力系统中，发电机内部的电压降和功率损失，以及传输系统，都是很小的。
• 这里，负载阻抗比源的内部阻抗高几倍
• 因此，功率电路工作在最优匹配条件下。例如，在电力传输中，最重要的是效率，所以我们设计的系统基于最高的电压。但是由于50%的损耗，无法抵抗散热，因为它提供的功率是100mw。

这都是关于最大功率定理的。从以上信息，最后，我们可以得出结论，这一定理经常用于保证最高的功率可以从电源传输到负载。这里有个问题，最大功率传递定理的优点是什么?