什么是网格分析:过程和例子

在bob足球体育app在美国，分析哪怕是简单的电路也更为重要。用于分析简单的电路、原理等Kirchhoff的电压和Kirchhoff的现行法律使用。而对于具有多个受控电压源和电流源的复杂电路，除了KVL和KCL定律外，还需要额外的工具。仅用KVL和KCL原理，分析结果是不准确和不可靠的。因此，为了进行精确的分析，并了解这些电路中的变量，必须实现网格和节点等方法。通过这些方法，可以很容易地知道电流和电压等变量。让我们在这篇文章中清楚的了解到Mesh Analysis, Super Mesh Analysis。

什么是网格分析?

网格被认为是环路中没有其他环路的环路。在这里，为了找出整个电路的分析，用网格电流代替电流作为变量。正因为如此，该技术需要解的方程数量最少。利用基尔霍夫电压定律对电路进行网格分析，得到未知的电流值。

这也被称为网格电流回路技术。在此之后，电压值也可以通过欧姆定律的实施而得到。分支被认为是连接两个节点的路径，它包含一个电路元件。当一个网格仅由一个支路组成时，则支路电流称为网格电流。而当一个网格由两个分支组成时，当两个分支路径相似或相反时，则认为网格电流是两个网格环路的和或差。

步骤

• 在了解电路的变量时，有一个执行网格分析的步骤，步骤可以解释如下:
• 在第一阶段，找出网格和标记网格电流在逆时针或顺时针方向。
• 查看流过对应于网状电流的每个元素的电流流量。
• 写下观察到的网格的所有网状方程。网格方程是通过应用Kirchhoff的法律来写的，然后通过申请欧姆法律来编写
• 找出网格电流，按照步骤3求解观察到的网格方程。
• 有了这个，电流和电压值的流动在电路中的每个元素可以知道应用网格电流。

在网格分析中建立方程的一般形式

在识别电路中的网格时，每个网格由一个方程组成。该方程是整个网电流回路中电压降的总和。对于大于电压和电流的电路，电压降被认为是阻抗乘以特定环网电流的电路。

当电压源存在于回路内部时，那么源处的电压可以根据电压损失或电压增加的条件进行加或减。而当电流源不在网格间时，则网格电流根据网格电流源方向考虑源的负或正值。

网眼电流方法

利用以下电路，可以容易地知道网格电流方法分析。在电路中，沿顺时针方向施加环路电流I1和I2

根据回路电流的方向，电压降的极性发生在电阻R1、R2和R3处。在这里，I1和I2电流将有相反的电流流动路径，因为电阻R2共享两个环路。

所以，电压的极性都是已知的。然而在实际应用中，R2可分为两相，但环电流特别适用于分析应用。对电压源的极性没有影响，因为它们是恒定的。

在Kirchhoff的电压法应用后，可以写入以下两个方程

R2(I1 - I2) + R1I1 = V1 -由循环1导出

R2(I2 - I1) + R1I2 = - v2 -由循环2推导而来

将上述方程中的相似项合并排列后，相同项出现在每个方程的相似位置。当环路电流已知时，就可以计算支路电流。重新排列的方程为:

I1（R1 + R2） - I2R2 = V1 - 用于循环1

-i1r2 +（r2 - r3）i3 = -v2 - 用于循环2

网格分析解决了问题

本节展示解决的示例使用网状电流方法在电路中找到电流．

在下面的电路中，通过网格分析方法找出通过15安培电流源的电压量。提供了所有的电流来源

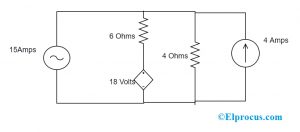
根据电路，存在使用并联电阻将电压源改变电压的可能性。除此之外，电阻器串联与电压源串联连接，电阻应具有与电压源相同的值，电压是

VS = ISRS = 4 * 4 = 16V

找出循环的分支电流（I1和I2），并在循环中表示当前流动方向。

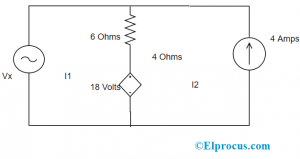
然后，对于每个网格(环)，应用KVL定律

网格 - 1

Vx - (I1 - I2) - 18 = 0

在这里，i1 = 15

所以Vx + (6 * I2) = 90

网格 - 2

18 - 6 (i2 - i1) - 4 * i2 - 16 = 0

I2 = 78/10.

= 7.8安培

根据网格-1方程

Vx = 90 - 44.4

Vx = 45.6 V

这是解决的例子使用网格电流分析解决两个网格

在这里，我们需要找出电压和分支电流。考虑以下电路。

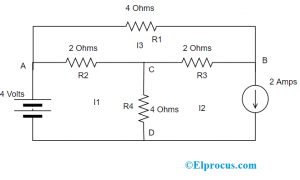
通过将KVL法应用于第一个循环，我们得到了

V1 - r2 (i1 - i3) - r4 (i1 - i2) = 0

4 - 2(i1) - 2(i3) - 4(i1) - 4(i2) = 0

-2(i3) - 6 (i1) = 4

将KVL定律应用于第二网格，得到

-VC - R4（I2 - I1） - R3（I2 - I3）= 0

- vc = -4(I1) + 6(I2) - 2 (I3) = 0

作为i2 = -2a，我们得到了

-vc = -4（i1）-12 - 2（i3）= 0

将KVL定律应用于第三网格，得到

- r1 (i3) - r3 (i3 - i2) - r2 (i3 - i1) = 0

代入I2 = -2A

2（i1） - 8（i3）= 0

但是解第一和第三个网格方程，我们得到

I1 = 4.46, I3 = -0.615

Vc = 28.61V

和分支电流是

IAC = I1 - I3

IAC = 5.075安培

这是解决的例子使用网格电流分析解决三个网格

这些是通过网眼分析解决的示例。对这一概念的彻底分析允许我们解决复杂电路。

超级网格分析

对于巨大和复杂电路的分析，超级网格分析作为比网格分析的最佳方法，因为在超级网格中，将有两个网格共享公共组件作为当前源。

同样的技术也适用于超级节点电路分析，作为节点电路分析的替代方案，因为这种方法通过关闭电压元件和最小化每个电压源的参考节点数量来简化那些复杂电路。在超网格分析中，电流源位于超网格区段的内部，因此对于存在的每一个电流源，可以使网格最小化一个。

当电流源出现在电路的允许器上时，则可能不考虑单个网格。另一方面，KVL仅针对修改后电路中的网格实现。

让我们考虑超级网格分析的例子为了更好的理解。

使用超级网格分析，找出以下电路的V3，I1，I2和I3的值？

在KVL的应用到网格-1，我们得到了

10i1 + 80(i1 - i2) + 30 (i1 - i3) = 80

得到60i1 - 20i2 - 30i3 = 80

通过应用超级网格技术来网2和网格3，我们得到了

30 =40i3+ 30 (i3 - i1) + 20(i2 - i1)

70i3 - 50i1+ 20i2 = 30

所述超网格中的单个电流源对应于所述超网格中的期望网格电流

15ix = i3 - i2

i3 = 15ix + i2

通过解决上述三个方程，我们得到了

i1 = 0.58安培，i2 = -6.16安培，i3 = 2.6安培

为了找到V3，我们有V3 = i3 * R3，所以

V3 = 2.6 * 40 = 104v

网格分析用途

网格分析最重要的用途是解析平面电路，以了解简单电路和复杂电路中任何位置的电流值

它的另一个用途是，通常的求解方程的计算是困难的，需要更多的数学公式，而通过网格分析，很少的计算就足够了。

网眼电流分析的其他用法是一个不平衡的小麦石桥。要了解这一点，请考虑以下示例

作为电阻器的比例，R1 / R4和R2 / R5不等于，我们可以理解，R3将存在一定量的电压和电流。如我们所知，通过综合串行技术的方法解决这些类型的电路，我们需要另一种方法来解决这个问题。

因此，在此方面，我们可以使用分支电流方法，但这种方法需要从IA到IA的六个电流，如果导致任何数量的方程式。因此，这种复杂性可以很容易地减少网目前的方法这只需要几个变量。