什么是抽样定理声明及其应用
一个信号有三个特性,例如电压或振幅,频率,阶段。信号仅以数字形式的模拟形式表示技术不可用。模拟信号在信号的不同时间和电压水平的差异中是连续的。这里,幅度的主要缺点是,幅度随着信号周期而变化。这可以通过数字形式的信号表示来克服。这里可以使用采样技术将信号的模拟形式转换为数字形式。该技术的输出代表其模拟信号的离散版本。在本文中,您可以找到什么是采样定理,定义,应用程序及其类型的采样。
什么是抽样定理?
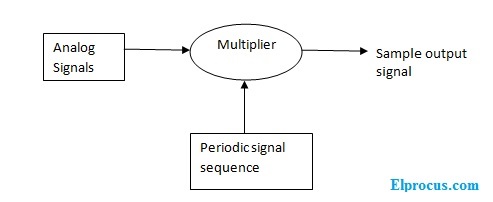
连续信号或连续信号模拟信号可以在数字版中以样本的形式表示。这里,这些样本也称为离散点。在采样定理中,输入信号是模拟信号,第二个输入信号是采样信号,它是一个脉冲序列信号,每个脉冲的周期为“t”。此采样信号频率应大于输入模拟信号频率的两倍。若满足此条件,则模拟信号完全可以用离散形式表示,否则模拟信号可能在一定时间间隔内失去其幅值。采样频率比输入模拟信号频率多多少倍,同样的,采样信号将是一个完美的离散信号。这些类型的离散信号在恢复原始信号的重建过程中表现良好。
抽样定理的定义
采样定理可以通过将采样频率从输入模拟信号频率的两倍定义为模拟信号的转换为分立形式。输入信号频率由FM表示和由FS表示的采样信号频率。
输出样本信号由样品表示。将这些样品保持在间隙,这些间隙被称为样品周期或采样间隔(TS)。采样周期的倒数称为“采样频率”或“采样率”。采样的样本数量表示在采样信号中由采样率表示。
采样频率fs = 1 / ts
抽样定理声明
采样定理指出,当具有更高频率的采样信号频率fs时,可以在样本的帮助下以示出的信号的离散形式表示时变形信号的持续形式可以用信号的离散形式表示,并且采样(离散的)信号可以恢复到原始形式值小于或等于输入信号频率fm。
Fs≥2调频
如果采样频率(FS)等于输入信号频率的两倍(FM),则这种情况称为采样的奈奎斯特标准。当采样频率等于输入信号频率的两倍时被称为“奈奎斯特速率”。
fs = 2fm.
如果采样频率(FS)小于输入信号频率的两倍,则此类标准称为混叠效果。
FS <2FM.
因此,存在来自采样频率标准的三种条件。他们是抽样,奈奎斯特和别名国家。现在我们会看到奈奎斯特采样定理。
奈奎斯特抽样定理
在采样过程中,在将模拟信号转换为离散版本的同时,所选择的采样信号是最重要的因素。在转换模拟到离散的同时,在采样输出中扭曲的原因是什么?这些类型的问题可以通过“奈奎斯特采样定理”来回答。
奈奎斯特采样定理指出,为了得到失真较小的输出信号,采样信号的频率应是输入信号最高频率分量的两倍。根据这位科学家的名字,哈里·尼奎斯特这叫做尼奎斯特抽样定理。
fs = 2fm.
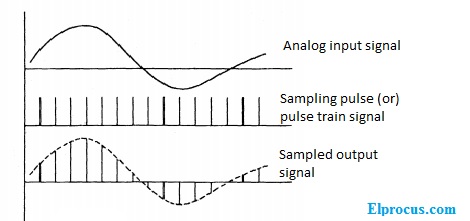
采样输出波形
采样过程需要两个输入信号。第一输入信号是模拟信号,另一个输入是采样脉冲或等距脉冲串信号。然后是采样信号的输出来自乘法器块。采样过程输出波形如下所示。
Shannon采样定理
抽样定理是模型中最有效的方法之一bob的是什么网站将模拟信号转换为离散和数字形式的概念。后来,数字电脑克劳德香农的进步,美国数学家实施了这个采样概念数字的bob的是什么网站用于转换模数到数字形式的通信。采样定理是通信中的一个非常重要的概念,这种技术应遵循奈奎斯特标准来避免锯齿效果。bob的是什么网站
应用程序
很少有抽样定理的应用如下所示。他们是
低通信号的采样定理
低通信号具有较低的频率范围,当这类低频信号需要转换为离散信号时,采样频率应是这些低频信号的两倍,以避免输出离散信号中的失真。在此条件下,采样信号不重叠,采样信号可以被重建到原始的形式。
- 信号带宽受限的xa (t)
- XA(T)的傅里叶信号表示XA(F)
抽样定理证明
采样定理指出,可以在样本的帮助下实现离散版本中的模拟信号的表示。参与该过程的输入信号是模拟信号和样本脉冲序列序列。
输入模拟信号为s(t) 1
样本脉冲序列为
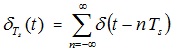
输入模拟信号的频谱是,
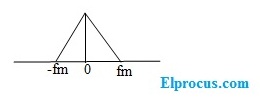
采样脉冲序列的傅里叶级数表示为

样品输出信号的频谱是,
当这些脉冲列序列是具有模拟信号的倍数时,我们将获得所用的采样输出信号,该输出信号在此表示为G(t)。
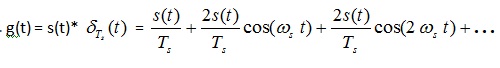
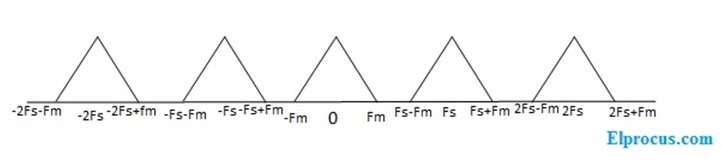
当与方程3有关的信号从LPF传递时,只有Fm到-Fm信号传递到输出侧,剩余的信号将被消除。因为LPF的截止频率等于输入模拟信号的频率值。通过这种方式,在一边模拟信号被转换成离散信号,并简单地从低通滤波器恢复到其原始位置。
因此,这是关于概述的采样定理。我有个问题要问你,奈奎斯特速率是多少?




