锯齿波发生器及其工作原理

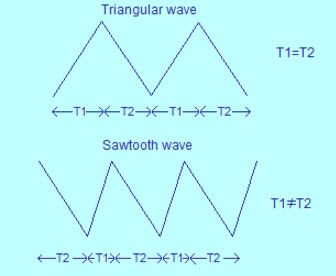
波形是表示相对于时间的幅度变化的形状。周期性波形包括正弦波，方波，三角波，锯齿波。在X轴上，它表示它指示幅度的时间和y轴。许多人经常在三角波和锯齿波之间混淆。锯齿波发生器是一种线性，非轴线波形，并且该波形的形状是三角形形状，其中下降时间和上升时间是不同的。锯齿波形也可以命名为非对称三角波。

锯齿波发生器

线性，非正弦，三角形波形表示锯齿波形，其中下降时间和上升时间是不同的。线性，非正弦，三角形波形表示纯三角波形，其中下降时间和上升时间等于。锯齿波发生器也称为非对称三角波形。锯齿波形的图形表示如下：

锯齿波形的应用包括频率/音调产生、采样、晶闸管开关、调制等。

非正弦波形不仅仅是锯齿波形。因为它的牙齿看起来像锯，所以它被命名为锯齿波形。在逆（或反向）锯齿波形中，波突然向下倾斜，然后急剧上升。

无穷傅里叶级数是

可以使用传统的锯齿

A是振幅

通过使用快速傅里叶变换，可以更有效地计算这个总和。在时域上，采用无频带限制形式数字化产生波形。采样无限次谐波结果的音调，其中包含混叠失真。

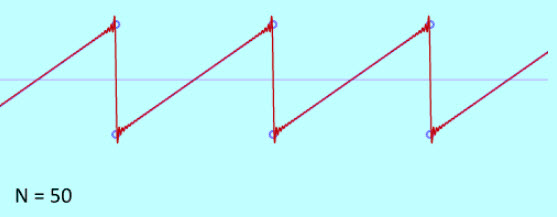
555锯齿波发生器的工作原理

一个锯齿波发生器可以用一个晶体管和一个简单的555定时集成电路，如下面的电路图所示。它包括晶体管，电容器，a齐纳二极管，来自用于给电容器充电的恒流源的电阻。首先，让我们假设电容器完全放电。电压跨电容是零，555的输出是高的，因为内部比较器连接到引脚2。

电容器开始充电以提供电压，因为555的内部晶体管短路电容器对地，它打开。在充电过程中，如果电压增加到供电电压的2/3以上，555输出就会下降。在放电过程中，如果C上的电压降低到1/3电源电压以下，555输出会变高。因此，电容器在电源电压的2/3到1/3之间充放电。但缺点是，它需要双相人格电力供应。频率由

f =（vcc-2.7）/（r * c * vpp）

在哪里，

VPP-峰值峰值输出电压

Vcc,电源电压

要获得所需的频率值，请为VCC，VPP，R和C选择适当的值

使用运算放大器的锯齿波发生器

中使用了锯齿波形脉冲宽度调制电路和时基发生器。当刮水器朝向负电压（-V）移动时，使用电位器;然后上升时间变得超过下降时间。当刮水器朝向正电压（+ V）移动时，上升时间变得小于下降时间。

当比较器输出变为负饱和时，将负电压添加到反相端子，从而刮水器移动到负电源。这导致R1上的电位差的降低，因此通过电容器和电阻器的电流降低。

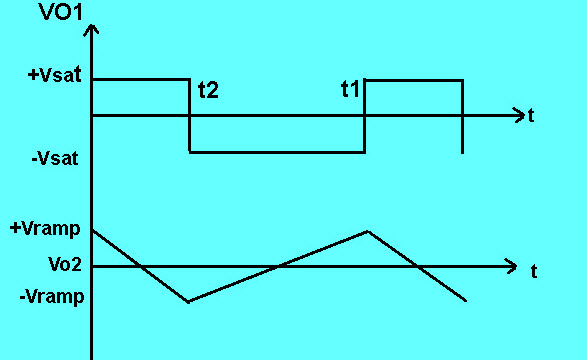
然后坡度降低，上升时间也降低。什么时候比较者输出处于正饱和状态，R1上的电位差增大，通过电容电阻的电流也增大。这是由于在反相端存在负电压所致。然后斜率增大，下降时间减小。输出为锯齿波形。

用于接线电路的元件如下:

• 运算放大器IC - 741 c
• R-47K.
• R1 - 1 k
• R2-180Ω

什么是正弦波?

描述平滑重复振荡的数学曲线称为正弦波或正弦波。它经常发生在纯和信号处理以及物理，化学，应用数学和许多其他领域。它是时间(t)的函数。当与其他任何相同频率、相位和幅值的正弦波相加时，正弦波保持其波形。我们知道它是一种具有这种性质的周期波形。这种重要性导致了它在傅里叶分析中的应用。

Y（x，t）= sin（kx-ωt+φ）+ d

a是幅度
ω = 2πf，是角频率
F是频率，它定义为每秒振荡的数量。
φ是相位角
D是非零中心幅度

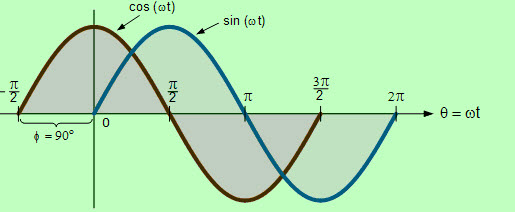
什么是余弦波？

余弦波的形状与正弦波的形状相同，除了余弦波精确地发生的比相应正弦波更早发生循环。正弦波和余弦波具有相同的频率，但余弦波引导正弦波90˚。

y = cos x

应用程序

• 锯齿波形是最常见的波形用于创建声音减法虚拟和模拟音乐合成器。因此，它被用于音乐中。
• 锯齿是水平和垂直偏转信号的形式，用于在显示器屏幕或基于CRT的电视上产生光栅。
• 磁场突然崩塌在波的悬崖上，这导致了它的电子束的静止位置尽可能快。
• 偏转轭产生的磁场将电子束拖曳在波的斜面上，形成一条扫描线。
• 由于频率较低，垂直偏转与水平偏转系统的工作方式相似。
• 电子元件的稳定性得到改善，因此无需调整画面的水平或垂直线性度。
• 正电压在一个方向上引起偏转;负电压在其他方面引起偏转，而位于中心的偏转使用屏幕面积来描绘一个轨迹。
• 斜坡部分必须出现为直线;否则，它表示由偏转轭产生的磁场，不是线性的。这导致非线性，电视图像被压低。因此，在图片的那一侧，电子束花费更多时间。

这都是关于锯齿波发生器和它的工作原理。我们相信本文提供的信息有助于您更好地了解这个项目。此外，对于与本文有关的任何查询或在实现电气和电子产品项目bob体育棋牌bob足球体育app，你可以在下面的评论区联系我们。这里有个问题，锯齿波发生器的工作原理是什么?

照片信用：

• 锯齿波发生器circuitstoday
• 使用运算放大器的锯齿波发生器博客网站
• 余弦波bob足球体育appelectronics-tutorials
• 锯齿波发生器的合成维基