总和的产品和产品总和

不同形式的规范表达，包括和总和（POS）和产品的产品和（POS）的总和，规范表达可以定义为一个布尔表达式要么有最小项，要么有最大项。例如，如果我们有两个变量，即X和Y，那么由最小项组成的正则表达式将是XY+X ' Y '，而由最大项组成的正则表达式将是(X+Y) (X ' +Y ')。本文讨论了乘积和和的乘积、SOP和POS的类型、原理图设计和K-map。

总和的产品和产品总和

概念的概念产品总和（SOP）主要包括流程、SOP类型、K-map、SOP方案设计。同样，和的乘积(POS)主要包括最大术语类型的,产品的金额，k映射和POS的原理图设计。

什么是产品的总和（SOP）？

乘积和的简写形式是SOP，它是一种布尔代数表达。在此，在一起添加不同的产品输入。输入的产品是布尔逻辑和而和或加法是布尔逻辑或。在理解乘积和的概念之前，我们先要知道中项的概念。

的最小期限可以定义为，当输入的最小组合是高的，那么输出将是高的。最好的例子是与门，所以我们可以说最小项是与门输入的组合。最小项真值表如下所示。

X	Y	Z	最小期限（M）
0	0	0	x'y'z'= m0
0	0	1	X没有'Z = m1
0	1	0	X ' y Z ' = m2
0	1	1	X 'YZ = m3
1	0	0	XY 'Z ' = m4
1	0	1	XY'z = M5
1	1	0	XYZ m6 ' =
1	1	1	XYZ = m7

在上表中，有三种输入，即X, Y, Z，这些输入的组合为8。每个组合都有一个指定为m的中项。

产品和的类型(SOP)

的和产品的可在三种不同的形式其中包括以下内容。

• 标准乘积和
• 非规范产品总和
• 最小的产品总和

1).产品规范和

这是标准的SOP形式，可以将o/p值高或为真的函数的项分组形成，也称为项和。规范SOP的表达式用符号求和(∑)表示，当输出为真时取括号中的项。标准乘积和的真值表如下所示。

X	Y	Z	F
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	0
1	1	1	0

对于上表，规范的SOP形式可以写成F =∑(m1, m2, m3, m5)
通过展开上面的求和，我们可以得到以下函数。
F = m1 + m2 + m3 + m5
代入上式中的项，可得下式
F = x ' y ' z + x ' yz + x ' yz + xy ' z
规范形式的产物术语包括补充和非称重的投入

2).非规范产品和

在非规范产品形式中，简化了产品项。例如，让我们采取上述规范表达。
F = x ' y ' z + x ' yz + x ' yz + xy ' z
f = x'y'z + x'y（z'+ z）+ xy'z
在这里z'+ z = 1（标准功能）
f = x'y'z + x'y（1）+ xy'z
F = x 'y 'z + x 'y + xy 'z
这仍然是SOP的形式，但它是非规范形式

3).最小乘积和

这是产品总和的最简化表达，而且它也是一种非规范的。用布尔代数简化了这种类型的可以简化定理虽然它只是通过使用K-map(卡诺图)。

由于输入线的数量而选择此表格使用门在这最小。由于其固体尺寸，快速速度，以及低制造价格，它是有利可图的。

让我们扮演一个规范形式函数的例子，并且最小产品总和K地图是

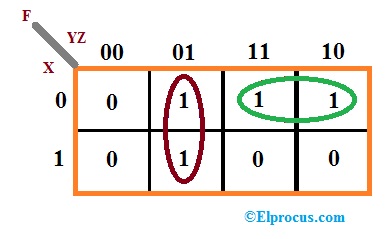
基于K-MAP的表达将是

f = y'z + x'y

产品和方案设计

产品总和的表达执行了两级和或设计，这种设计需要集合和栅极和一个或门。产品总和的表达式类似的设计。

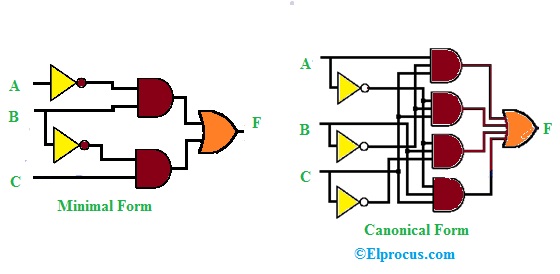
输入的数量和与门的数量取决于一个正在实现的表达式。使用AND-OR门的最小乘积和规范表达式的设计如上所示。

什么是和的乘积(POS)?

和乘积的简写形式为POS，是布尔代数的一种表达式。在这种情况下，它是不同输入和的乘积的一种形式，它们不是算术结果和，尽管它们对应于逻辑布尔与或。在理解和乘积的概念之前，我们必须知道最大项的概念。

maxterm可以定义为对于最大数量的输入组合为真，否则对于单个输入组合为假。因为“或”门也只对一个输入组合提供假值。因此，最大项是任何补全或非补全输入的OR。

X	Y	Z	马克斯术语(M)
0	0	0	x + y + z = m0
0	0	1	X + Y + Z = M1
0	1	0	x + y'+ z = m2
0	1	1	X + Y + Z = M3
1	0	0	X + Y + Z = M4
1	0	1	X + Y + Z = M5
1	1	0	x'+ y'+ z = m6
1	1	1	X + Y + Z ' = M7

在上表中，有三种输入，即X, Y, Z，这些输入的组合为8。每个组合都有一个用M表示的最大项。

在最大术语中，每个输入都补充，因为它仅在应用规定的组合时提供“0”，而Minterm的补充是最大术语。
M3 = M3 '
（x'yz）'= m3
x + y'+ z'= m3（de morgan的法律）

和积(POS)的类型

和的乘积分为以下三种类型。

• 总和的规范产品
• 和的非标准积
• 和的极小积

1)和的标准乘积

规范POS也被命名为最大术语的产品。这些是和共同的，o / p低或假。当输出为假时，拍摄由π表示的表达式和括号中的最大术语。总和的规范产品的真实表如下所示。

X	Y	Z	F
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	0
1	1	1	0

对于上表，可以写入规范POSf =π（m0，m4，m6，m7）
通过展开上面的方程，我们可以得到以下函数。
F = m0, m4, m6, m7
通过在上面的等式中取代最大术语，我们可以获得以下表达式
F = (x + y + z)(x ' + y ' + z)(x ' + y ' + z)(x ' + y ' + z ')
规范形式的产物术语包括补充和非称重的投入

2）。非规范产物的总和

表达总和的产品（POS）非规范形式称为非规范形式。例如，让我们用上面的表达式
F = (x + y + z)(x ' + y ' + z)(x ' + y ' + z)(x ' + y ' + z ')
F = (y + z) (x ' + y ' + z) (x ' + y ' + z ')
类似的，尽管反向的术语从两个Max term & forms中移除，这里只显示一个实例term。
=（x + y + z）（x'+ y + z）
= xx'+ xy + xz + x'y + yy + yz + x'z + yz + zz
= 0 + xy + xz + x'y + yy + yz + x'z + yz + z
= x (y + z) + x ' (y + z) + y (1+ z) + z
= y + z (x + x ') + y (1) + z
= (y + z) (0) + y + z
= Y + Z
上述最终表达式仍为和积的形式;然而，它是非规范的形式。

3）。和的极小积

这是和的乘积最简化的表达式，也是一种非规范的类型。这种类型的罐是由布尔代数定理简化，虽然它是简单地使用k -映射(卡诺映射)。

由于输入线的数量和栅极的数量，选择此表格是最小的。由于其固体尺寸，快速速度，以及低制造价格，它是有利可图的。

让我们扮演一个规范形式函数的例子，而且K映射和的乘积是

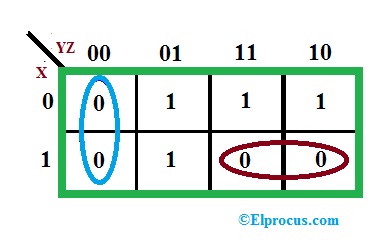
基于K-MAP的表达将是

f =（y + z）（x'+ y'）

乘积和的原理图设计

该总和的乘积的表达执行了两个级别或 - 设计，并且该设计需要集合或门和一个和门。该总和的每个表达式都有类似的设计。

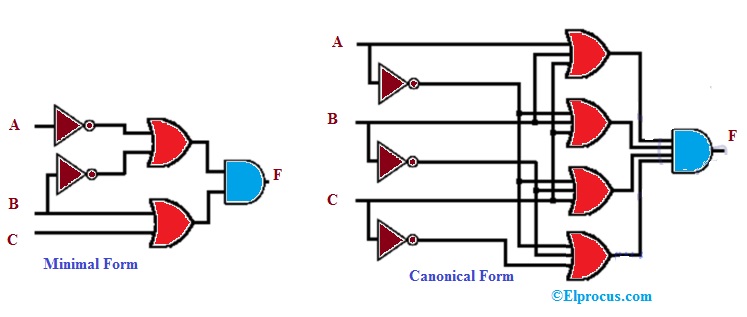
输入的数量和与门的数量取决于一个正在实现的表达式。使用或 - 和门的最小产品和典型表达的设计如上所述。

因此，这一切都是关于规范形式:积和与积、原理图设计、k -图等。最后从上面的信息，我们可以得出结论，一个布尔表达式完全由任何minterm组成，否则maxterm被命名为规范表达式。我有个问题要问你两种形式的规范表达是什么？