什么是叠加定理：限制及其应用

对于每一个电路，都有两个或额外的独立电源，如电流、电压或两个电源。检查这些电路， 这叠加定理广泛利用，主要用于各种频率的时域电路。例如，线性DC电路包括一个或多个独立电源;我们可以使用像网格分析和节点分析技术等方法获得电压和电流等电源。否则，我们可以采用“叠加定理”，其中包括每个供应结果的值为待决定的价值。这意味着定理假设电路中的每个电源独立地发现变量的速率，并且通过插入由每个来源的效果的变量来产生辅助变量。即使它的过程非常困难，但仍然可以应用于每个线性电路。

什么是叠加定理？

叠加定理是一种用于独立用品的方法电路像电压和电流，当时被认为是一个电源。本定理据说，在包括一个或多个源的线性N / W中，电路中通过多个电源的电流流是当独立地代理源时电流的代数计算。

本定理的应用涉及简单的线性N / WS，也涉及AC和DC电路，其中它有助于构建电路等“诺顿“ 也 ”戴维南“等效电路。

例如，具有两个或更多个电源的电路，然后电路将基于叠加定理的陈述分离为多个电路。这里，分离电路可以使整个电路在更简单的方法中似乎非常简单。并且，通过在单个电路修改后的另一个时间合并分离电路，可以简单地发现节点电压等因素，电阻等电压，电流等。

逐步定位定理声明方法

以下逐步方法用于通过叠加定理发现特定划分中的电路的响应。

• 通过允许一个独立的供应来计算电路特定分支的响应以及删除网络中的电流。
• 对电路中所有的电压和电流源重复上述步骤。
• 包括所有的反应，以获得一个特定的电路中，当所有的供应在网络中。

应用叠加定理的条件是什么？

将该定理应用于网络必须满足下列条件

• 电路元件必须是线性的。例如，电流与施加在电路上的电阻的电压成正比;磁链可以与电感器的电流成正比。
• 电路组件必须是双侧，这意味着电压源的相反极性中的电流流必须是相同的。
• 在这个网络中使用的元件是无源的，因为它们没有放大或整流。这些元件是电阻，电感和电容器。
• 不应使用有源组件，因为它们永远不会很少线性以及从未是双边的。这些组件主要包括晶体管，电子管和半导体二极管。

叠加定理示例

叠加定理的基本电路图如下所示，这是本定理的最佳示例。通过使用该电路，计算通过电阻器R的电流流量为以下电路。

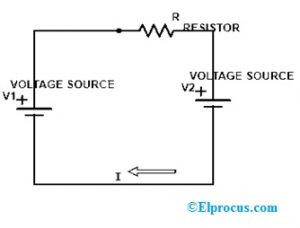
禁用辅电压源I.E，V2，并计算下面电路中的电流I1的流量。

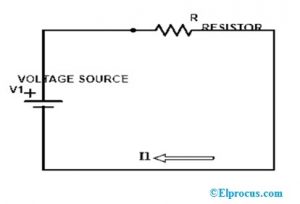
我们知道欧姆法律v = IR

i1 = v1 / r

禁用初级电压源I.E，V1，并计算以下电路中的电流I2流。

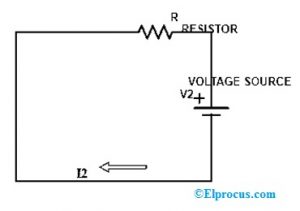
I2 = - v2 / R

根据叠加定理，网络电流I = I1 + I2

i = v1 / r-v2 / r

如何使用叠加定理?

以下步骤将告诉您如何应用叠加定理来解决问题。

• 在电路中占据一个来源
• 通过短路更换电压源，剩余独立源必须设置为零，而带开路的电流源
• 离开独立来源
• 作为第一步中首选的单一源的结果，计算整个所需分支的电流方向和幅度。
• 对于每个电源，从第一步到第四个步骤重复这些步骤，直到测量到所需的支路电流，因为电源单独作用。
• 对于所需的分支，使用方向添加所有组件电流。对于AC电路，需要完成相位量。
• 要测量电路中任何元件的电压，需要遵循相同的步骤。

叠加定理问题

以下电路显示了用于解决叠加定理问题的基本DC电路，使得我们可以获得负载端子上的电压。在以下电路中，有两个独立的供应即电流和电压。

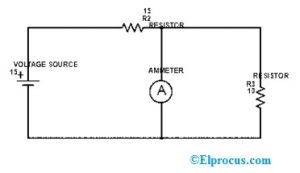
最初，在上述电路中，我们保持仅电压是作用的，并且电流的剩余电源随内部电阻而变化。因此，上述电路将成为下图所示的开路电路。

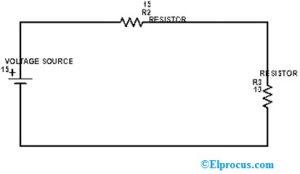
考虑负载端子VL1两端的电压，电源单独执行，然后

VL1 = VS（R3 /（R3 + R1））

这里，vs = 15，r3 = 10和r2- = 15

请将上述数值代入上述方程

VL1 = vs×R3 /（R3 + R2）

= 15（10 /（10 + 15））

15 (10/25)

= 6伏

仅保持电流电源，并通过其内部电阻改变电压供应。因此，电路将成为一个短路，如下图所示。

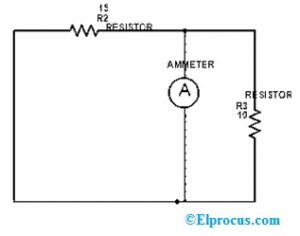
考虑负载端子上的电压是“VL2”，而电流电源执行。然后

vl2 = i x r

IL = 1 x R1 /（R1 + R2）

R1 = 15 rl = 25

= 1×15 /（15 + 25）= 0.375安培

VL2 = 0.375 × 10 = 3.75伏

结果，我们知道叠加定理指出负载上的电压是VL1＆VL2的量

VL = VL1 + VL2

6 + 3.75 = 9.75伏特

叠加定理的先决条件

叠加定理可简单地应用于每一个电源在同一时刻可简化为串联或并联的电路。所以这不适用于检查不平衡桥电路。它只适用于线性基本方程。
线性需求只需确定电压和电流仅适用于。该定理不用于电路，其中任何部件的电阻通过电流变化否则否则电压。

因此，不能评估包括诸如气体放电或白炽灯的部件的电路，否则无法评估压敏电阻。本定理的另一个要求是电路中使用的组件应该是双侧的。

本定理在研究中使用交流(交流)电路以及半导体电路，其中交流电流经常通过DC混合。作为AC电压以及电流方程，与直流相似的线性。因此，该定理用于使用DC电源检查电路，之后具有AC电源。结果将结合起来，以说明这两个来源都将发生什么。

叠加定理实验

叠加定理的实验可以如下所做的。下面讨论该实验的逐步步骤。

目标

用下面的电路实验验证叠加定理。这是一种分析方法，用于确定电路中使用多个电源的电流。

设备/所需组件

该电路的装置是面包板，连接线，毫米电流表，电阻等。

实验理论

当电路包括两个或更多个源时，简单地使用叠加定理。本定理主要用于缩短电路的计算。本定理指出，在双边电路中，如果像两个或以上一样使用多个能源，则电流的流程将在任何点处存在，并且它是所有电流的总和。

流量将在每个源单独考虑的点&其他源将通过阻抗改变，这是等价于它们的内部阻抗。

电路图

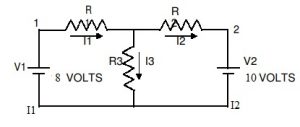
程序

下面讨论该实验的逐步过程。

• 连接直流电源供应跨越1＆I1的端子和施加的电压为V1 = 8V且同样地，跨越电压电源V2为10伏的终端
• 测量所有支路的电流，它们是I1, I2和I3。
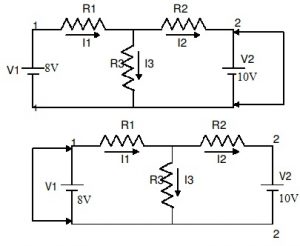
• 首先，将电压源V1 = 8V连接在1到I1和短路端子的端子上，横跨2到I2为V2 = 0V。
• 通过毫安计计算V1 = 8V和V2=10V所有支路的电流。这些电流用I1 '、I2 '和I3 '表示。
• 同样，连接唯一的V2 =10伏跨2到I2端子以及短路端子1和I1, V1=0。用毫安计计算两个电压在所有支路的电流，用I1”、I2”和I3”表示。

为了验证叠加定理，

i1 = i1' + i1“

I2 = I2'+ I2'

I3 = I3 ' + I3”

测量理论电流值，这些值必须与测量的电流值相等。

观察表

这values of I1, I2, I3 when V1= 8V & V2 =10V, the values of I1’, I2’ & I3’ when V1= 8V and V2=0 and for the values, I1’’, I2’’ & I3’’ when V1=0 & V2=10V.

v1 = 8v. V2 = 10 v	v1 = 8v. v2 = 0v.	v1 = 0v. V2 = 10 v
I1	I1'	I1''
I2	I2'	I2''
I3	I3'	I3''

结论

在上述实验中，由于剩余电压源短路，分支电流仅仅是由于单独的电压源的电流的代数总和;因此，本定理已被证明。

限制

叠加定理的局限性包括以下几点。

• 本定理不适用于测量功率，但它测量电压和电流
• 它用于线性电路，但不用于非线性
• 当电路必须高于一个源时，应用该定理
• 对于不平衡的桥接电路，它不适用
• 本定理不用于功率计算，因为可以基于线性地完成本定理的工作。因为功率方程是电流和电压的乘积，否则否则电压或电流平方，而不是线性。因此，不可实现通过电路内的元件利用的电力。
• 如果负载选件是可变的，否则负载电阻定期变化，则需要实现电压或电流的每个源贡献以及负载电阻内的每个变换的总和。因此这是分析困难电路的一个非常困难的过程。
• 叠加定理对功率计算不有用，但本定理适用于线性的原则。由于电力方程不是线性的。结果，不可实现的电路中的因子中使用的功率是不可实现的。
• 如果负载选择是可变的，那么需要实现每个供应捐赠及其在负载电阻中变换的计算。因此，这是分析复合电路的一种非常困难的方法。

应用程序

这叠加定理的应用是，我们只能使用线性电路以及具有更多供应的电路。

从以上叠加定理的例子可以看出，该定理不适用于非线性电路，而适用于线性电路。电路可以在同一时间用单一电源进行检查

等效截面电流和电压代数包括发现他们将在每一个电源的作用。若要抵消除一个电源外的所有电源，可用电缆代替任何电源;用断路器恢复任何电流供应。

因此，这一切都是关于叠加定理概述这说明，通过使用这个定理，我们可以在一个时间只使用一个电源分析电路，相关的分量电流，以及电压，可以添加代数来观察他们将实现什么有效使用所有电源。为了抵消所有的电源，只保留一个电源供分析，然后用导线改变任何电压源，通过开路(断路)改变任何电流源。我有个问题要问你，什么是KVL?