不同类型的Chebyshev过滤器，具有计算

Chebyshev过滤器的名称在“Pafnufy Chebyshev”之后被称为，因为其数学特征仅来自他的名称。Chebyshev过滤器只不过是模拟的或数字过滤器。这些过滤器具有陡峭的滚动和型式1滤波器（更多通过带纹波）或类型-2滤波器（停止频带纹波）Butterworth滤波器。此筛选器的属性是，它会降低实际和理想化过滤器的特性之间的错误。因为，在此过滤器中的通带纹波所固有的。

Chebyshev过滤器

Chebyshev过滤器用于另一个频段的不同频率。它们无法匹配Windows-Sink过滤器的性能，它们适用于许多应用程序。Chebyshev滤波器的主要特点是它们的速度，通常比窗口-Sinc更快。因为这些过滤器由递归而不是卷积执行。Chebyshev和Windowed-Sinc滤波器的设计取决于称为Z变换的数学技术。

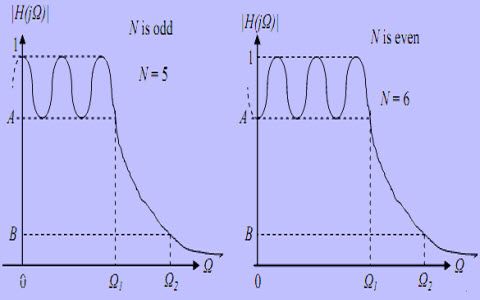
Chebyshev过滤器的类型

Chebyshev过滤器分为两种类型，即Type-i Chebyshev Filter和Type-II Chebyshev Filter。

Type-i Chebyshev过滤器

这种类型的过滤器是Chebyshev过滤器的基本类型。幅度或增益响应是LPF（低通滤波器）的第n级的角频率函数等于传递函数HN（JW）的总值

GN（W）= | HN（JΩ）| =1√（1 +ε2Tn2（）ω/ωo）

其中，ε=纹波因子
ωo=截止频率
TN =第n个订单的Chebyshev多项式

通频带显示平均性能。在该频带中，滤波器在-1＆1之间交换，因此在G = 1 /√（1 +ε2）时MAX在G = 1和min之间的滤波器交换的增益。在截止频率下，增益具有1 /√（1 +ε2）的值，并且随着频率的增加，仍然失败进入止动频带。过滤器的行为如下所示。-3dB的截止频率通常不适用于Chebyshev滤波器。

此过滤器的顺序类似于否。Chebyshev滤波器需要的反应性能量模拟设备。DB中的纹波是20LOG10√（1 +ε2）。因此，如果在止动杆中允许在复杂平面中的JW轴上允许在止动杆中允许纹波，则可以找到由ε= 1的幅度的幅度的幅度的幅度。虽然，这种效果在止动杆上的抑制不太抑制中。该效果称为Cauer或椭圆滤波器。