什么是高通滤波器？电路图，特性和应用

有一个时代的时候，在打电话的时候，距离的距离，人们必须把嘴放在靠近发射器，非常慢慢地说话，以便在另一端的人清楚地听到消息。今天，我们甚至可以通过高质量分辨率在全球范围内进行视频通话。这种巨大发展的技术的秘诀在于电过滤器理论和传输线理论．电子滤波器是一种电路，它只通过选定的频带，而衰减其他不需要的频率。其中一个过滤器是高通滤波器．

什么是高通滤波器？

高通滤波器的定义是仅通过其频率高于截止频率的信号的过滤器，从而衰减较低频率的信号。截止频率的值取决于过滤器的设计。

高通滤波电路

基本的高通滤波器由串联连接构建电容和电阻．当输入信号被应用到电容器，输出绘制电阻器．

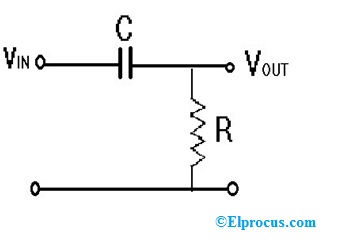
在这种电路安排中，电容器在较低频率有高的电抗，因此它对低频输入信号起到开路的作用，直到达到截止频率' fc '。滤波器将所有信号衰减到截止频率水平以下。在频率以上的截止频率水平电容的抗变低，它作为一个短路的这些频率，从而允许他们直接通过到输出。

无源RC高通滤波器

上面所示的高通滤波器也被称为被动RC高通滤波器由于电路仅限使用被动元素．无需应用外部电源以进行过滤器。这里电容器是反应元件，并在电阻上绘制输出。

高通滤波器特性

当我们谈论时截止频率我们指的是滤波器的频率响应如果增益等于50％的信号.i.e的峰值增益。峰值增益的3DB。在高通滤波器中，增益增加随着频率的增加而增加。

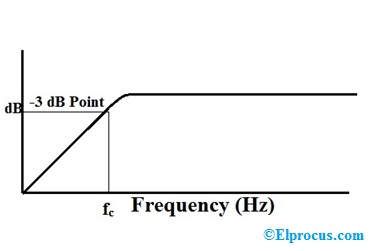
该截止频率FC取决于电路的R和C值。这里，恒定τ= Rc，截止频率与时间常数成比例。

截止频率=1/2πRC

电路增益由AV = VOUT / VIN

.i.e。AV = (Vout)/(V in) = R/√(R²+ XC²）= r / z

低频F：XC→∞，Vout = 0

高频F：XC→0，Vout = Vin

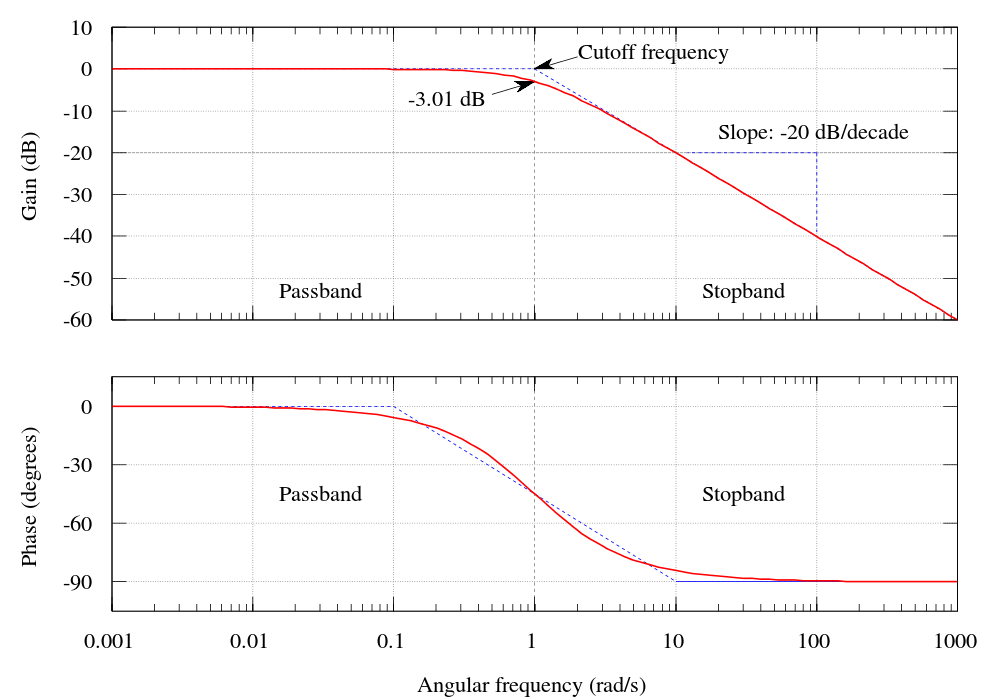
高通滤波器频率响应或高通滤波器BODE图

在高通滤波器中，抑制截止频率'FC'下方的所有频率都衰减。在这种切断频率点，我们得到-3db增益，并且在电容器的电差和电阻值的情况下将相同.i.e。r = xc。收益计算为

GAIN（DB）= 20日志（VOUT / VIN）

高通滤波曲线斜率为+20 d B/ 10年。通过截止频率电平后，电路的输出响应以每10年+20 dB的速率从0增加到Vin，即每八度增加6 dB。

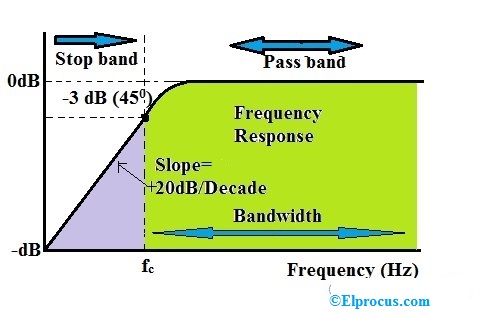
从初始点到截止频率点的区域称为停止频带，因为不允许频率通过。从截止频率上方的区域。即-3 dB点被称为通频带．在截止频率下，点输出电压幅度为70.7％的输入电压。

这里过滤器的带宽表示允许信号通过的频率的值。例如，如果高通滤波器的带宽给出为50kHz，则意味着只允许从50kHz到无穷大的频率通过。

输出信号在截止频率处的相位角为+450。计算高通滤波器相移的公式为

∅=反正切⁡(1/2πfRC)

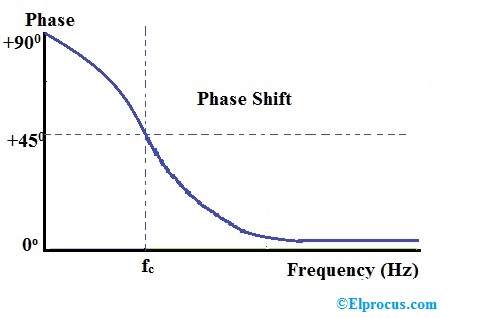
在实际应用中，滤波器的输出响应不会延伸到无穷大。滤波器元件的电特性将限制应用于滤波器响应。By proper selection of filter components, we can adjust the range of frequencies to be attenuated, the range to be passed etc…

使用运放的高通滤波器

在这个高通滤波器和无源滤波器元素，我们添加op-amp.到电路。在此，输出响应不受开环的限制而不是获得无限输出响应。OP-AMP的特征．因此，这个过滤器充当一个带通滤波器截止频率，由带宽定义和OP-AMP的增益特性。

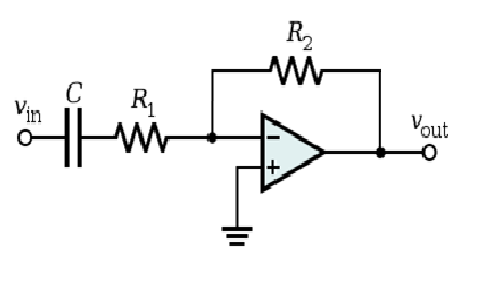
OP-AMP的开环电压增益充当带宽的限制放大器．放大器的增益随着输入频率的增加而降低到0 dB。电路的响应类似于被动高通滤波器，但这里的OP-AMP的增益放大了输出信号的幅度。

这过滤器的增益使用非反相运算放大器是由:

AV = VOUT / VIN =（AF（F / FC））/√（1+（F / FC）^ 2）

AF是滤波器=的通带增益1+（R2）/ R1

f是Hz中输入信号的频率

FC是切断频率

当低耐受性时电阻和电容器使用这些高通有源滤波器提供了良好的精度和性能。

有效高通滤波器

使用运放的高通滤波器也被称为一个有效高通滤波器因为除了无源元件，电容和电阻还有一个有源元件OP-AMP用于电路．使用此活动元素，我们可以控制滤波器的截止频率和输出响应范围。

二阶高通滤波器

我们看到的过滤电路全部被认为是一阶高通滤波器。在二阶高通滤波器中，将额外的RC网络块添加到一阶高通滤波器在输入路径。

二阶高通滤波器

这二阶高通滤波器的频率响应类似于第一阶高通滤波器。但是，在二阶高通滤波器停止频段将是40dB /十年的第一阶滤波器的两倍。可以通过级联和二阶滤波器来形成高阶滤波器。虽然订单没有限制，但过滤器的大小随着顺序和精度降低而增加。如果在高阶滤波器R1 = R2 = R3等中...并且C1 = C2 = C3 =等......然后截止频率如何相同，而不管滤波器的顺序如何。

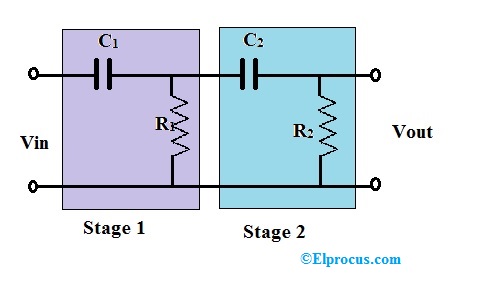
可以给出二阶高通有源滤波器的截止频率

Fc = 1 /（2π√（R3 R4 C1 C2）））

高通滤波器传递函数

随着电容器的阻抗频繁地改变，电子滤波器具有频率依赖性响应。

给出了电容器的复杂阻抗佐= 1 / sC

其中，S =Σ+jω，ω是每秒弧度的角频率

可以使用标准电路分析技术（如）找到电路的传递函数欧姆的法律那Kirchhoff的法律那叠加等式的转移函数的基本形式

H (s) = (s ^ m +一个(m - 1) ^ (m - 1) +⋯+ a0) / (bn s ^ n + b (n - 1) s ^ (n - 1) +⋯+ b0)

这过滤器的顺序由分母的次数可知。杆和零通过求解等式的根来提取电路。该功能可能具有真实或复杂的根。这些根在S平面上绘制的方式，其中σ由横轴表示，ω用垂直轴表示，显示有关电路的大量信息。对于高通滤波器，零位于原点。

Vout/Vin = (-Z2 (jω))/(Z1 (jω))

= - R2 /（R1 + 1 /Jωc）

= 1/(1+ 1/(jωR1 C))

这里h（∞）= r2 / r1，ω→∞的增益

τ = R1 C和ωc= 1/(τ)ωc = 1 / (R1C)是截止频率

因此，高通滤波器的传递功能由h（jω）= - h（∞）（1 /（1+ 1 /Jωτ））

= - h（∞）（1 /（1-（jΩc）/ω）））

当输入频率低时，Z1（JΩ）很大，因此输出响应低。

当ω=0时，H(jω) = (- H(∞))/√(1+(ωc/ω)^2) =0;H(∞)/√2当ω=ω_c;

H（∞）当ω=∞时。这里负符号表示相移。

当R1 = R2，S =JΩ和H（0）= 1时

因此，高通滤波器的传递函数H(jω) = jω/(jω+ ω_c)

黄油值高通滤波器

理想的滤波器除了可以排除不需要的频率外，还应该对需要的频率具有均匀的灵敏度。这种理想的过滤器是不切实际的。但是Stephen Butter worth在他的论文《关于滤波器放大器的理论》中指出，这类滤波器可以通过增加合适大小的滤波器元件的数量来实现。

黄油值过滤器以这样的方式设计，使得它在过滤器的通带中提供平坦的频率响应，并且在止动频带中朝向零。一个基本的原型黄油值过滤器是低通设计但通过修改高通和乐队通过过滤器可以设计。

正如我们上面看到的一阶高通滤波器单元增益H（jω）=jΩ/（jω+ω_c）

对于串联的N这样的滤波器h（jω）=（jω/（jω+ω_c））^ n在解决方面时

'n'控制通带和停止频段之间的转换顺序。因此，顺序越高，快速过渡所以，在n =∞黄油的价值滤波器变为理想的高通滤波器。

在这个滤波器的实现过程中，为了简单起见，我们考虑ωc = 1并求解传递函数

为了S = jω .即H(s) = s/(s+ωc) = s/(s+1)为订单1:

H(s) = s²/(s²+∆ωs+(ωc²))订购2.

因此高通滤波器中级联的传递函数为

高通滤波器的应用

高通滤波器应用主要包括以下内容。

• 这些过滤器用于扬声器进行放大。
• 高通滤波器用于去除接近可听范围低端的不需要的声音。
• 防止放大直流电流这可能损害放大器，高通滤波器用于交流耦合。
• 高通滤波器图像处理:高通滤波器用于图像处理，以锐化细节。通过在图像上应用这些过滤器，我们可以夸大图像中的每一个微小细节。但过度使用会损害图像，因为这些过滤器会放大图像中的噪声。

这些过滤器的设计方面仍有很大的发展，以实现稳定和理想的结果。这些简单的设备在各种各样的控制系统，自动系统，图像和音频处理。哪个应用程序高通滤波器你遇到过吗？