什么是史密斯图表：基础知识，类型及其应用

Smith图表是两个研究员的菲利普史密斯和Tosaku的发明，他们在这个图表发现中占据了个别学分。该图表是在贝尔电话的研究实验室的20世纪30年代开发的。筹集的所有工程并发症都是由这个史密斯图解析，直到期间数字电脑突出。当史密斯图表的商标已过期时，MS。史密斯在2015年将商标销售给IEEE MTT社会。理查德Syssdr博士还参加了这些商标讨论以及史密斯女士。因此，观察到史密斯图表具有MTT-S背景。因此，这是史密斯图表的简要介绍，让我们清楚地了解本文中的图表概念。

什么是史密斯图表？

史密斯图被认为是一种图形测量工具，主要用于电气工程师来解决与之相关的问题RF传输线路和匹配的设备。同时，该装置还用于显示进纳，连续增益概要，阻抗，稳定性，噪声系数等各种因素，也显示了机械振动的详细分析。

图表在使用半径范围为1或<1的区域内更常见，例如在稳定性性能和振荡器设计的情况下。如众所周知，用于解决复杂数学问题的史密斯图表的使用施加匹配问题，但它仍然是解释RF频率在多个频率级别执行的有效方法。这是因为大多数RF电路软件由史密斯图表组成，用于显示结果。

史密斯图表的类型

史密斯图绘制了复杂反射系数平面上的两个维度，并且图表通常以阻抗或导纳或甚至通过多种颜色标准化，以便在这些参数之间区分，并且根据该缩放，这些主要分为三种类型。那些是

阻抗史密斯图表

这些通常被称为通常类型的史密斯图表，因为它们对应阻抗并以优异的方式起作用，即使具有许多串联组件的巨大负载，其中这些是阻抗匹配中的重要组成部分和其他RF对应的操作。这种阻抗是主要类型，其中其他类型被认为是其衍生物。代表阻抗史密斯图表的图片如下所示：

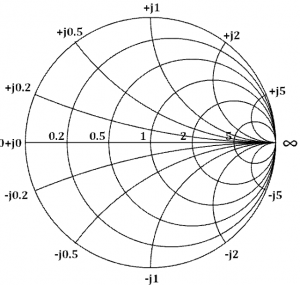
入场史密斯图表

在处理串联负载时，阻抗图表是至关重要的，这里的所有功能都是最大限度地求出整个阻抗。虽然这里的棘手部分是处理元素的并行元素时的数学计算电感器，传输线和电容器。

因此，为了最大限度地减少阻抗图表所涉及的并发症，这些进入图表是开发的。由于我们都意识到入场具有对阻抗的重视关系，因此该进入图表适用于复杂的并行情景。为此，必须清楚地分析天线入场，而不是阻抗，并简单地汇总所有这些。代表这两个因素（阻抗和导纳）之间关系的等式是：

y =（1 / z1）= c +是

这里的“y”对应于负载进入，“Z”对应于阻抗。

'C'是电导，并且''是遗传。

等式本身表明阻抗和导纳保持反向关系。

图片如下所示：

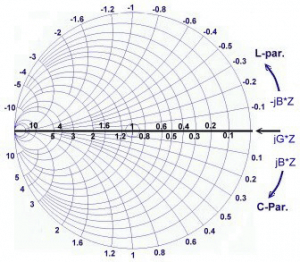
犹豫史密斯图表

我们都讨论了阻抗史密斯图表更有用来处理序列组件，导纳史密斯图表适用于并行组件。但是，在这种组件的实施情况下，情况变得复杂和棘手。对此的答案是犹太史密斯图。这是一个有效的解决方案，在另一个方面绘制阻抗和导纳图。下面是图片。

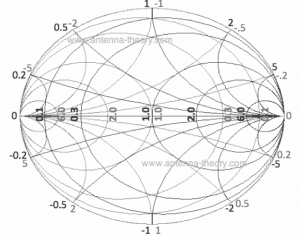
此图表有助于合并阻抗和入境图表的能力。在阻抗匹配操作中，它有助于了解序列或并联元素如何影响阻抗，以最小的努力。

基本

由于已经说明，史密斯图表在极性形式中表现出特定负载阻抗的复杂反射系数。我们都知道阻抗被称为总和电抗并且抵抗并且以相同的方式，反射系数也是复差数字，也表示为负载阻抗'ZL'和参考阻抗'Z0'。

上述陈述的数学表示是

=（ZL - Z0）/（ZL + Z0）=（ZL-1）/（ZL + 1）

这里，'z0'corr对应的发送器阻抗，并且'zl'对应于负载阻抗。主要是对应于频率的天线阻抗的图形表示可能是单个或几个点。这个理论对应于史密斯图的基础图。

组件

由于有许多线条，该图表的图形表示似乎有些典型。但是当我们了解每行的概念时，图表非常容易实现。

对于阻抗史密斯图，有两个圆圈定义了史密斯图的信息和设计，它是恒定的r圈和恒定的x圆圈。

常数r圈子

这里，初始一组线被称为恒定电阻线，其中全部在水平半径的右手处彼此相邻位置。当阻抗的电阻保持恒定时，这些圆圈出现，并且X值变化。由此，常数R圆上的整个点将具有类似的电阻值。

所有这些点都在其交叉点的水平线上突出显示。这通常表示为圆的直径。图片如下所示：

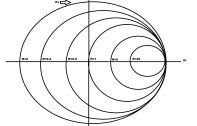
例如：当归一化阻抗表示为zl = r + ix时，当r等于'0'时，x等于任何真正的积分，那么

ZL = 1 + I0，ZL = 1 + I3和ZL = 1 + I4

恒定x圈子

这里，该曲线包括比圆的更多弧，并且所有这些弧处于在水平半径的右边缘处彼此的切向位置。当阻抗的电抗保持恒定时，这些圆圈出现，并且X值变化。

在上半部分部分中的线表示反应的正值，而下半部分的线条表示反应的负值。

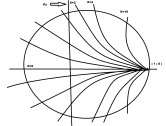
例如，当曲线表示为zl = r + iy并且当y = 1并且常数保持并且r表示到0到无穷大的实际积分，然后恒定x圆形图如下所示。这些是史密斯图的组件。

应用程序

在RF工程的任何域中，史密斯图表具有各种应用。史密斯图表的最重要应用是

• 它用于传输线用于计算在任何负载提供的阻抗
• 甚至采用该图表来计算在任何负载提供的进入值
• 用于测量Tx.line的短路部分的长度，以便提供所需的电容电感抗抵抗量
• 用于阻抗匹配的目的
• 雇用了解其他人之间的价值。

史密斯图在阻抗匹配中的应用

要使用史密斯图表并找出结果，需要正确了解交流电路和传输线的概念，其中这些代表RF工程的先决条件。要了解更多信息，让我们考虑一个例子如何使用史密斯图表进行阻抗匹配在传输线和天线的情况下。

在这里，图表的应用是找出组件（电容器或电感器）值，其确保正确匹配线，因此反射系数为“0”。

例如，当阻抗值被认为是Z = 0.5-0.6J时。最初，我们需要知道图表上具有0.5值的电阻圆。由于阻抗值是负的，这意味着我们表示电容阻抗，我们需要在0.5值电阻圈上以逆时针方向移动它，以了解它触摸负0.6电抗弧的点。这提供了有助于将线路匹配到负载的组件的值。

标准化缩放让Smith图表在具有代表图表的焦点的任何独特或系统阻抗的应用中实现。在阻抗图表的情况下，通常使用的归一化阻抗值是50欧姆，其中用于简单地描绘阻抗。

当通过此发现结果时，我们可以通过乘以导纳价值来直接在归一化阻抗和相关的非正式化值之间转换。利用这种反射，可以易于知道系数。另外，这些还用于解决这些并发症，这些并发症具有阻抗和终止的频率值的变化。

易于解决一次具有一个频率值的问题，而在带宽应用的情况下，它似乎具有多种频率的复杂性。这通过Smith图表解决，结果显示为轨迹，所有频率范围彼此接近。这些基因座点对应于此

• 电感或电容负载如何通过所确定的频率范围变化
• 如何具有多个频率水平的复杂匹配
• 如何正确匹配组件。

因此，这就是史密斯图表用于阻抗匹配。

总的来说，这是关于史密斯图的概念。本文提供了清晰的史密斯图表描述，其类型，组件，基础，阻抗和入场史密斯图表。为了获得对这一概念的更详细知识，通过各种各样史密斯图示例。