什么是互感及其理论

1831年，迈克尔法拉第解释了理论电磁感应科学地。术语电感是导体的容量，以反对流过它并诱导EMF的电流。从法拉第的归纳定律，诱导电动势（EMF）或电压指挥由于磁场通过电路的变化。该过程称为电磁感应。感应电压与电流的变化率相反。这被称为Lenz的定律，并且诱导电压被调用回EMF。电感分为两种类型。它们是自感和互感。本文是关于两个线圈或导体的互感。

什么是互感？

定义：两个线圈的互感被定义为由于一个线圈中的磁场引起的EMF而反对另一个线圈中的电流和电压的变化。这意味着由于变化，两个线圈在一起磁性连接在一起磁性助焊剂。一个线圈与另一个线圈连杆的磁场或通量。这是由M.表示的

在一个线圈中流动的电流由于磁通量的变化而在另一个线圈中引起另一个线圈中的电压。连接的与两个线圈连接的磁通量与互感和电流变化成正比。

相互电感理论

它的理论非常简单，可以通过使用两个或更多个线圈来理解。它是由美国科学家约瑟夫亨利在18世纪描述。它被称为电路中使用的线圈或导体的特性之一。物业电感是，如果电流在一个线圈中随时间变化，则EMF将引起另一个线圈。

奥利弗省去了1886年的术语电感。相互电感的财产是许多人的工作原则电气元件与磁场一起运行。例如，变压器是互感的基本示例。

互感的主要缺点是，一个线圈的电感泄漏可以使用电磁感应来中断另一个线圈的操作。为了减少泄漏，需要电气筛选

电路中的两个线圈的定位决定将与另一个线圈的相互电感的量。

互感公式

给出了两个线圈的公式

m =（μ0.μR.n1。n2。a）/ l

其中μ0=自由空间的渗透率=4π10-²

μ=软铁芯的渗透率

n1 =线圈1的转弯

n2 =线圈2的转弯

a = M中的横截面积²

l =线圈的长度为米

相互作用单位

相互电感的单位是kg。m²。^-2。一个^-2

由于1pplere /秒的电流变化率，电感量产生了一伏的电压。

该SI单位相互电感是亨利。它是从美国科学家约瑟夫亨利解释了两个线圈的现象。

相互电感的尺寸

当两个或更多个线圈用相同的磁通量磁通地连接在一起时，在一个线圈中感应的电压与另一个线圈中的电流的变化率成比例。这种现象被称为相互电感。

考虑两个线圈之间的总电感是l，因为m =√（l1l2）= l

这的尺寸可以定义为电位差与电流变化率的比率。它被给予

由于m =√l1l2= l

l =€/（di / dt）

其中€=诱导的EMF =相对于时间的工作/电荷= M. L²。t²/它= m.l².t-3。一世^-1或€= m. l^-2。T-3。一个^-1（因为我= a）

对于电感，

φ= li.

l =φ/ a =（b。l²） / 一个

其中b =磁场=（mlt-²）/ LT.^-1AT = MT.^-2一个^-1

磁通Φ= BL²= Mt.^-2L.²一个^-1

B和φ的替代值高于公式l

l = mt-²L.²。一个^-2

给出L1和L2时相互电感的尺寸给出

m = l /（t-²L.²。一个^-2）

m = lt.²L.²。一个^-2

衍生

遵循这个过程来获得互感推导。

在一个线圈中诱导的EMF的比率和另一个线圈中电流的变化率是相互电感的。

考虑两个线圈L1和L2，如下图所示。

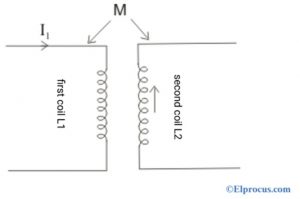
当L1中的电流随时间而改变时，磁场也随着时间而改变并且改变与第二线圈L2连接的磁通量。由于该磁通量改变，在第一线圈L1中感应EMF。

而且，第一线圈中的电流的变化率在第二线圈中引导EMF。因此，EMF在两个线圈L1和L2中感应。

这是给出的

€= m（di1 / dt）

m =€/（di1 / dt）。...... eq 1

如果¥= 1伏特和DI1 / DT = 1AMP，那么

m = 1亨利

也，

一个线圈中电流的变化率在第一线圈中产生磁通量，并与第二线圈相关联。然后，从法拉第的电磁感应定律（感应电压与磁通量的磁通量的变化率直接成比例）在第二线圈中，诱导的EMF给出

€= m /（di1 / dt）= d（mi1）/ dt ... .. eq 2

€= n2（dφ12/ dt）= d（n2φ12）/ dt ... eq 3

通过等同于等式2和3

mi1 =n2φ12

m =（n2φ12）/ i1 henry

其中m =相互电感

€=互感EMF

n2 =第一线圈L1中的匝数

i1 =第一个线圈中的电流

φ12=在两个线圈中连接的磁通量。

两个线圈之间的互感取决于第二线圈或相邻线圈上的匝数，以及横截面的区域

两个线圈之间的距离。

由于磁通量的变化率，在第一线圈中引起的EMF是给出的，

e = -m12（di1 / dt）

当EMF被诱导时，减号表示对第一线圈中电流变化率的反对。

两个线圈的互感

通过将它们放置在柔软的铁芯上或通过增加两个线圈的匝数来增加两个线圈的互感。当它们在软铁芯上紧密缠绕时，两个线圈之间存在团结耦合。磁通量泄漏将很小。

如果两个线圈之间的距离短，则在第一线圈中产生的磁通量与第二线圈的所有转弯相互作用，这导致大的EMF和互感。

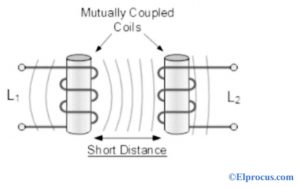
如果两个线圈以不同的角度彼此彼此更远，则第一线圈中的感应磁通量在第二线圈中产生弱或小的EMF。因此，相互电感也将很小。

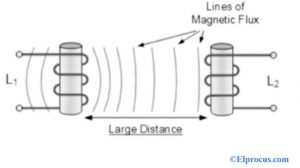
因此，这的价值主要取决于两个线圈在软铁芯上的定位和间隔。考虑该图，表明两个线圈在软铁芯顶部紧密缠绕。

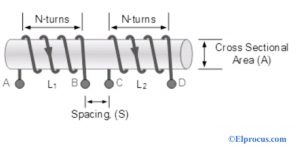
第一线圈中的电流的变化产生磁场并通过第二线圈通过第二线圈，用于计算互感。

给出了两个线圈的互感为

M12 =（n2φ12）/ i1

m21 =（n1φ21）/ i2

其中M12 =第一线圈的互感到第二线圈

M21 =第二条线圈的互感到拳头线圈

n2 =第二个线圈的转弯

n1 =第一个线圈的转弯

i1 =电流在第一个线圈周围流动

I2 =电流在第二线圈周围流动。

如果与L1和L2连接的通量与周围流动的电流相同，则给出第一线圈到第二线圈的互感为M21

两个线圈的互感可以定义为m12 = m21 = m

因此，两个线圈主要取决于两个线圈之间的尺寸，转动，位置和间隔。

第一线圈的自感是

l1 =（μ0.μR.n1².a）/ l

第二线圈的自感是

L2 =（μ0.μR.n².a）/ l

交叉乘以上述两个公式

然后给出它们之间存在的两个线圈的互感

m²= L1。L2

m =√（l1.l2）亨利

上述等式给出磁通量= 0

L1和L2之间100％磁耦合

耦合系数

将与两个线圈连接到线圈之间的总磁通量的磁通量的磁通量被称为耦合系数，它由'k'表示。耦合系数被定义为开路与实际电压比的比率以及线圈中获得的磁通量的比率。由于一个线圈的磁通量与另一个线圈连接。

耦合系数指定电感器的电感。如果系数耦合k = 1，则两个线圈紧密地耦合在一起。所以，一个线圈的所有磁通量的磁通线切割另一个线圈的所有转弯。因此，相互电感是两个线圈的各个电感的几何平均值。
如果两个线圈的电感相同（L1 = L2），则两个线圈之间的互感等于单个线圈的电感。这意味着，

m =√（l1。l2）= l

其中L =单个线圈的电感。

线圈之间的耦合因子

线圈之间的耦合因子可以表示为0和1

如果耦合因子为1，则线圈之间没有电感耦合。

如果耦合因子为0，则线圈之间存在最大或完全电感耦合。

电感耦合在0和1中表示，但不是百分比。

例如，如果k = 1，则两个线圈完全耦合

如果k> 0.5，则两个线圈紧密耦合

如果K <0.5，则两个线圈耦合松散。

为了找到两个线圈之间的系数耦合因子，应该应用以下等式，

k = m /√（l1。l2）

m = k。√（l1。l2）

其中L1 =第一线圈的电感

L2 =第二线圈的电感

m =相互电感

K =耦合因子

应用程序

该相互电感的应用是，

• 变压器
• 电动机
• 发电机
• 其他电气设备，与磁场合作。
• 用于计算涡流的计算
• 数字信号处理

因此这一切都是关于互感概述- 定义，公式，单位，推导，耦合因子，系数耦合和应用。这是一个问题，两个线圈之间的互感缺点是什么？